18.Отрицание Операция инверсия (отрицание):

Отрицание - это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.

Обозначается: ол

В естественном языке: соответствует словам "неверно, что..." и частице "не"

Диаграмма Эйлера-Венна:

Принимаемые значения: лрл

Диаграмма Эйлера-Венна: В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества соответствует множество, дополняющее его до универсального множества.

Пример: Луна — спутник Земли (А). Луна — не спутник Земли ( A)

Отрица́ние в логике — унарная операция над суждениями, результатом которой является суждение (в известном смысле) «противоположное» исходному. Обозначается знаком ¬ перед или чертой над суждением. Синоним: логическое "НЕ".

Как в классической, так и в интуиционистской логике «двойное отрицание» ¬¬A является следствием суждения A, то есть имеет место тавтология: .

Обратное утверждение верно в классической логике (закон двойного отрицания), но не имеет места в интуиционистской. То есть, отрицание отрицания искомого утверждения не может служить интуиционистским доказательством, в отличие от классической логики. Это различие двух логических систем обычно полагается главным.

Схемотехника

Основная статья: Логические элементы — отрицание

Инвертор

0	1
1	0

Мнемоническое правило для отрицания звучит так: На выходе будет:

• "1" тогда и только тогда, когда на входе «0»,

• "0" тогда и только тогда, когда на входе «1»

19. импликация или функция следования

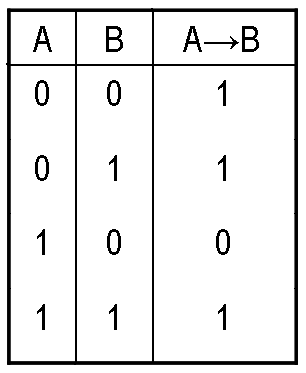
IV. Логическое следование (импликация).

Сложное логическое высказывание , образованное с помощью связки 'ЕСЛИ..., ТО...' называют логическим следованием или импликацией. Обозначают:

Для логического следования таблица истинности выглядит так:

20.сложение по модулю 2

Сложение по модулю 2.

Запись читается как a плюс по модулю 2 b.

Функция сложения по модулю 2 истинна тогда и только тогда, когда значения переменных различны.

а b a b

0 0 0

0 1 1

1 0 1

1 1 0

Выражение для сложения по модулю 2 можно записать в виде a b = •b +а•.

21 Функция тождества или эквиалентность

Функция тождества или эквивалентность а~b.

Истинна тогда и только тогда, когда значения переменных совпадают

а b a ~ b

0 0 1

0 1 0

1 0 0

1 1 1

22.Функция Шеффера

4. Функция штрих Шеффера (И-НЕ): Y = X1|X2 = NOT(X1X2)

Таблица истинности функции И-НЕ имеет вид:

 

Логический элемент И-НЕ обозначается на схемах следующим образом:

 

23. СТРЕЛКА ПИРСА

3. Функция стрелка Пирса (ИЛИ-НЕ): Y = NOT(X1+X2)

Таблица истинности функции ИЛИ-НЕ имеет вид:

 

Логический элемент ИЛИ-НЕ обозначается на схемах следующим образом:

 

24.Единичная Функция 1

Единичная функция 1 определяет логическую константу 1.

а b 1

0 0 1

0 1 1

1 0 1

1 1 1

1(a, b) = 1

25. нулевая функция 0

Нулевая функция 0 определяет логическую константу 0.

а b 0

0 0 0

0 1 0

1 0 0

1 1 0

26 и 27 в телефоне

28.основные и дополнительные законы алгебры логики

 1. Комплементарность.

     

  a  ·a' = 0;                                                         a + a' = 1

 

Доказательство: 0 and 1 = 0;  1 and 0 = 0;             0 or 1 = 1;  1 or 0 = 1

 

     2. Идемпотентный закон.

    

   a ·a =а;                                                          а + а=а

 

Доказательство: 0 and 0 = 0;  1 and 1 = 1             0 or 0 = 0;  1 or 1 = 1

 

     3. Переместительный закон.

   

    а + в = в + а;                                                   а·в = в·а

 

От перемены мест слагаемых или множителей результат не меняется.

 

     4. Сочетательный закон.

   

    (а + в) + с = а + (в + с);                                 (а·в) ·с = а· (в·с)

 

Если над аргументами функции выполняются однотипные логические действия, то их можно произвольно группировать (объеденять), изменяя последовательность действий.

 

     5. Закон поглощения.

 

        а + а·в = а· (1 + в) = а;                                    а· (a + в) = а + ав = а

 

Вынесем общий множитель в. Зная, что 1 + в = 1, получим:   а and 1 =  а

 

     6. Распределительный закон.

       а(в + с) = ав + ас;                                             а + вс = (а + в)(а + с)

     7. Закон склеивания

    

       ав + ав' = а;                                                 (а + в)(а + в') = а

Если один из аргументов изменяется при неизменном результате (функции), то этот аргумент можно исключить из выражения. Это один из самых важных законов, часто используемых для минимизации логических функций.

Задание. Самостоятельно доказать первую часть закона склеивания, используя распределительный закон.

Задание. Самостоятельно доказать вторую часть закона склеивания, используя распределительный закон и закон поглащения.

 

Доказательство: (а + в)(а + в') = а + ав + ав' + вв' = а + а(в + в') + 0 = а + а·1 = а + а = а