10. Перевод чисел из одной системы счисления в другую.

Для более компактной записи чисел обычно используются восьмеричная и шестнадцатеричная системы счисления. Поэтому большое практическое значение имеют процедуры перевода из одной системы счисления в другую. 

Правила перевода из одной  позиционной системы в другую
1. Перевод целого числа из десятичной системы счисления в систему счисления с основанием Q	осуществляется  последовательным делением данного  числа на основание Q, до тех пор, пока частное не станет равным нулю. Число в новой системе (S=Q) будет представлено в виде остатков от деления, записанных начиная с последнего.      Например, десятичное число 2210 запишется в двоичной системе следующим образом          Остаток      22:2 = 11        (0)      11:2 = 5        (1)      5:2 = 2         (1)      2:2 = 1         (0)      1:2 = 0         (1)             2210=101102.
2. Перевод правильной дроби из десятичной системы счисления в другую систему с основанием Q	осуществляется  последовательным умножением ее на основание новой системы счисления. Целая часть полученного числа будет первой цифрой после запятой. Дробную же часть необходимо вновь умножить на Q. Целая часть полученного числа будет следующей цифрой и т. д.
3. Для  перевода неправильных дробей в новую систему счисления	необходимо, с  помощью рассмотренных выше правил 1 и 2, отдельно выполнить перевод целой и дробной части.
4. Перевод чисел в десятичную систему счисления	осуществляется  путем составления степенного ряда с основанием той системы счисления, из которой это число переводится.

2. Правила перевода чисел из одной системы счисления в другую.

1. Перевод чисел из десятичной системы счисления в систему с основанием два

Рассмотрим два способа перевода числа из десятичной системы в другую на примере системы с основанием 2.

1). Способ разложения числа по степеням основания рассмотрим на примере перевода числа из десятичной системы счисления в двоичную. Для этого способа необходимо знать таблицу степеней числа 2:

2² = 4, 2³ = 8, 2⁴ = 16, 2⁵ = 32 , 2⁶ = 64, 2⁷ = 128, 2⁸ = 256, 2⁹ =512, 2¹⁰ = 1024,…

Переведем число 567₁₀ в двоичную систему. Определим максимальную степень двойки, такую, чтобы два в этой степени было меньше или равно исходному числу. В нашем случае это 9, так как 2⁹=512, а 2¹⁰=1024, что больше начального числа. Таким образом, мы получим число разрядов результата. Оно равно 9+1=10. Поэтому результат будет иметь вид 1ххххххххх, где вместо х могут стоять любые двоичные цифры. Найдем вторую цифру результата. Возведем двойку в степень 9 и вычтем из исходного числа: 567–2⁹=55. Остаток сравним с числом 2⁸=256. Так как 55 меньше 256, то девятый разряд будет нулем, т. е. результат примет вид 10хххххххх. Рассмотрим восьмой разряд. Так как 2⁷=128>55, то и он будет нулевым.

Седьмой разряд также оказывается нулевым. Искомая двоичная запись числа принимает вид 1000хххххх. 2⁵=32<55, поэтому шестой разряд равен 1 (результат 10001ххххх). Для остатка 55–32=23 справедливо неравенство 2⁴=16<23, что означает равенство единице пятого разряда. Действуя аналогично, получаем в результате число 1000110111₂. Исходное число мы разложили по степеням двойки:

567=1*2⁹+0*2⁸+0*2⁷+0*2⁶+1*2⁵+1*2⁴+0*2³+1*2² +1*2¹+1*2⁰

2). Способ деления на основание требуемой системы счисления является универсальным. Рассмотрим то же самое число 567. Разделив его на 2, получим частное 283 и остаток 1. Проведем ту же самую операцию с частным 283. Получим частное 141, остаток 1. Опять делим полученное частное на 2, и так до тех пор, пока частное не станет меньше делителя. Теперь для того, чтобы получить число в двоичной системе счисления, достаточно записать последнее частное, то есть 1, и приписать к нему в обратном порядке все полученные в процессе деления остатки.

 

Результат не изменился: 567 в двоичной системе счисления записывается как 1000110111. Эти два способа применимы при переводе числа из десятичной системы в систему с любым основанием.

2. Перевод чисел из десятичной системы в систему счисления с основанием 16

Переведем число 567 в 16-ричную систему счисления.

1). Используем разложение числа по степеням основания. Искомое число будет состоять из трех цифр, т. к. 16² = 256  <  567  <  16³ = 4096.

Определим цифру старшего разряда. 2*16²=512<567<3*16²=768, следовательно, искомое число имеет вид 2хх, где вместо х могут стоять любые шестнадцатеричные цифры. Остается распределить по следующим разрядам число 55 (567‑512). 3*16=48<55<4*16=64, значит, во втором разряде находится цифра 3. Последняя цифра равна 7 (55‑48). Искомое шестнадцатеричное число равно 237.

2) Способ последовательного деления на основание требуемой системы счисления приведет к тому же результату. Процесс деления заканчивается, когда частное становится строго меньше 16. Необходимо заменять 10 на A, 11 на B и так далее.

 

3. Перевод чисел из любой системы счисления в десятичную систему

В основе этого метода находится правило, что любое десятичное число можно представить в виде

x = a₀*pⁿ + a₁*p^n-1 + ... + a_n-1*p¹ + a_n*p⁰,

где a₀ ... a_n –это цифры данного числа в системе счисления с основанием p.

Пример.

Переведем число 4A3F₁₆ в десятичную систему.

По определению,

4A3F= 4*16³+A*16²+3*16+F.

Заменив A на 10, а F на 15, получим 4*16³+10*16²+3*16+15= 1900710.

4. Перевод чисел из двоичной системы в системы с основанием, равным степеням двойки (8 и 16), и наоборот

Проще всего осуществляется перевод чисел из двоичной системы в системы с основанием, равным степеням двойки (8 и 16), и наоборот. Для того чтобы целое двоичное число записать в системе счисления с основанием 2ⁿ, нужно число разбить справа налево на группы по n цифр в каждой. Если в левой группе окажется меньше n разрядов, то дополнить ее нулями до нужного числа разрядов. Рассмотреть каждую группу, как n разрядное двоичное число, и заменить ее соответствующей цифрой в системе счисления с основанием 2ⁿ.

1). Перевод восьмеричных чисел в двоичную систему: следует каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр).

Пример.

573,1₈ =101  011  111 , 001₂

               5       3       7       1

2). Перевод шестнадцатеричных чисел в двоичную систему: достаточно каждую цифру заменить эквивалентной ей двоичной тетрадой (четверкой цифр).

Пример.

1А3,F₁₆ = 0001  1010  0011 , 1111₂

                     1       A         3      F

3). Перевод числа из двоичной системы в восьмеричную: разбить влево и вправо от запятой на  триады, и каждую триаду заменить восьмеричной цифрой.

10101001,10111₂ = 010  101  001 , 101  110 ₂ = 251,56₈

                                 2       5       1       5       6

4). Перевод числа из двоичной системы в шестнадцатеричную: разбить влево и вправо от запятой на тетрады, и каждую тетраду  заменить шестнадцатеричной цифрой.

Пример.

10101001,10111₂ = 1010  1001 , 1011  1000 ₂ = A9B8₁₆

                                    A      9          B      8

5. Перевод правильных дробей из десятичной системы счисления в систему с другим основанием

Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого.

Пример.

Перевести 0.3125₁₀ в восьмеричную систему счисления.

 

Результат: 0.3125₁₀ = 0.24₈

Замечание. Конечной десятичной дроби в другой системе счисления может соответствовать бесконечная (иногда периодическая) дробь. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности.

Пример.

Перевести 0.65₁₀ в двоичную систему счисления с точностью 6 знаков.

 

Результат: 0.65₁₀

6. Перевод неправильных десятичных дробей в систему счисления с другим основанием

Необходимо отдельно перевести целую часть и отдельно дробную.

Пример.

Перевести 23.125₁₀ в двоичную систему счисления.

1) Переведем целую часть:	2) Переведем дробную часть:

 

 

Таким образом:  23₁₀ = 10111₂; 0.125₁₀ = 0.001₂.

Результат:  23.125₁₀ = 10111.001₂.

Необходимо отметить, что целые числа остаются целыми, а правильные дроби ‑ дробями в любой системе счисления.

11.каковы правила выполнения арифметических операций с двоичными числами

Сложение. Таблица двоичного сложения предельно проста. Только в одном случае, когда производится сложение 1+1, происходит перенос в старший разряд.

Пример 1 Рассмотрим несколько примеров сложения двоичных чисел:

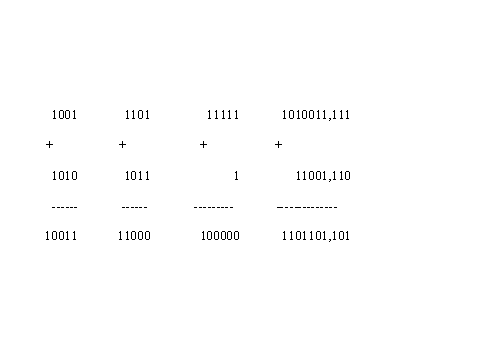
Вычитание в двоичной системе счисления. Исходя из того, что вычитание есть действие, обратное сложению, запишем правило арифметического вычитания одноразрядных чисел в двоичной системе счисления:

0 – 0=0; 1 – 0=1; 1 – 1=0; 10 – 1=1.

Используя это правило, можно проверить правильность произведенного выше сложения вычитанием из полученной суммы одного из слагаемых. При этом, чтобы вычесть в каком-либо разряде единицу из нуля, необходимо “занимать” недостающее количество в соседних старших разрядах (так же, как в десятичной системе счисления поступают при вычитании большего числа из меньшего).

Вычитание. При выполнении операции вычитания всегда из большего по абсолютной величине числа вычитается меньшее и ставится соответствующий знак. В таблице вычитания 1 с чертой означает заем в старшем разряде.

Пример 2. Рассмотрим несколько примеров вычитания двоичных чисел:

10111001,1-10001101,1=101100,0

101011111-110101101= -1001110

Умножение в двоичной системе счисления. Правила умножения одноразрядных двоичных чисел наиболее очевидны:

0 0=0; 1 0=0; 0 1=0; 1 1=1.

Умножение. Операция умножения выполняется с использованием таблицы умножения по обычной схеме, применяемой в десятичной системе счисления с последовательным умножением множимого на очередную цифру множителя.

Пример 3. Рассмотрим несколько примеров умножения двоичных чисел:

11001*1101=101000101

11001,01*11,01=1010010,0001

Вы видите, что умножение сводится к сдвигам множимого и сложениям.

 

Деление в двоичной системе счисления осуществляется так же, как и в десятичной, с использованием умножения и вычитания.

Деление. Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления.

Пример 4. Рассмотрим пример деления двоичных чисел:

101000101:1101=11001