57. Правила построения простой контрольной карты средних арифметических значений и медиан

Контрольные карты средних арифметических значений и медиан позволяют обнаруживать разладку процесса в том случае, когда генеральное среднее m контролируемого показателя качества x изменяется от значения m₀ при налаженном состоянии технологического процесса до значения m₁ при разлаженном состоянии процесса.

В качестве значения m₀ обычно используют номинальное значение контролируемого показателя качества x или же значение, соответствующее середине поля допуска. Значения m₁ и m_-1 – это предельно допустимые значения, которым соответствует предельно допустимый уровень дефектности.

Таким образом, по выборочному среднему арифметическому при заданном уровне значимости необходимо проверить гипотезу:

H₀ : m = m₀ о равенстве математического ожидания m заданному значению m₀ при конкурирующей гипотезе H₁ : m = m₁ или m _-1.

В качестве статистического критерия проверки нулевой гипотезы о математическом ожидании нормально распределённой случайной величины при известной дисперсии используется случайная величина

(2.71)

Если случайная величина x распределена нормально при справедливости нулевой гипотезы, математическое ожидание этой случайной величины M(U)=0, а (U) = 1. Следовательно, для нахождения критической точки можно использовать таблицу функции нормированного нормального распределения Ф(x).

Для двухсторонней критической области критическая точка U_кр находится по таблице функции нормального распределения из условия

(2.72)

Тогда условием принятия нулевой гипотезы будет выполнение неравенства

или

откуда

(2.73)

Таким образом, процесс будет признаваться налаженным до тех пор, пока выборочное среднее арифметическое не превысит значений границ регулирования, т.е.

‒ для ВГР;

‒ для НГР.

Если контролируемый показатель качества X только увеличивается либо только уменьшается, то строится контрольная карта с одной границей регулирования или 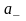соответственно, определяемыми из условий Ф(U_кр) = 1 ‒  и Ф(U_кр) =  соответственно.

Планы контроля для статистического регулирования ТП иногда строят в зависимости от средних длин серий выборок для налаженного и разлаженного состояний процесса, которые для простых контрольных карт соответственно равны (при односторонней критической области)

и (2.73)

Для получения плана контроля кроме значений L₀ и L₁ мы должны еще иметь значение , которое определяется из условия и характеризует уровень разладки процесса.

Итак, исходными величинами для выбора плана контроля при статистическом регулировании методом средних арифметических значений являются:

L ₀ , L ₁ (или  , ); m₀ , m₁ или m _-1 , .

При этих значениях, используя специальные таблицы (например, таблицу 4.1), находят объем выборки n и коэффициент , который необходим для вычислений границы регулирования. Значение , если оно неизвестно, может быть оценено по выборке большого объема в ходе предварительного анализа ТП.

Если использовать метод медиан, то границы регулирования и объемы выборок рассчитываются аналогично с заменой на . С учетом этого границы регулирования определяются:

. (2.74)

Таблицы для определения n и строят аналогично таблицам плана контроля методом средних арифметических значений.

Таким образом, статистическое регулирование ТП методом средних арифметических и медиан заключается в следующем:

- периодически отбираются выборки заданного объема n;

- измеряются показатели качества единиц продукции из этой выборки;

- по результатам этих измерений определяют выборочное среднее или выборочную медиану ;

- значения или отмечают на соответствующих контрольных картах;

- ТП признается налаженным, если отмеченные точки не выходят за границы регулирования или ;

- ТП признается разлаженным, как только первая из точек достигнет границы регулирования или превысит ее.

Пример 4. ТП изготовления подложек ГИС является налаженным, если средняя толщина подложки m₀ = 2,5мм и разлаженным, если m₁ = 2,52мм. Предварительным анализом предыдущего процесса установлено, что =0,02мм. Задано также L₀ = 20, L₁ = 1,25. Необходимо осуществить статистическое регулирование с помощью контрольных карт средних арифметических значений.

Решение:

1. Определим степень разладки ТП:

.

2. Для значений  = 1, L₀ = 20, L₁ = 1,25 по таблице 4.1 определяем

и .

3. Так как разладка процесса определяется лишь одним увеличением m, то можно определить лишь одну границу регулирования:

.

Наладку ТП контролируют периодически путем изъятия выборок из 6 подложек и вычисления среднего арифметического значения . Данные значения наносят на контрольную карту. Как следует из графика, приведенного на рисунке 2.21, после 6-й выборки процесс будет признан разлаженным.

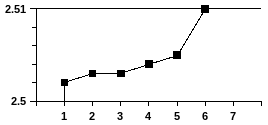
Рисунок 2.21 – Контрольная карта средних арифметических значений