38. Функция распределения показательного распределения (вывод), ее график.

F(x)= ) = 0, x <0

=1-e-^λx –^λx x ≥0 График:

39.Вероят попадания в задан интервал для показат распред: P(L<X<B)=F(B)-F(X)=(1-e ^-λB) – (1-e- ^λx)=1 - e ^–λB -1+e- ^λx = e- ^λx - e^-λB

P(L<X<B)= = e- ^λx - e^-λB

40. Математическое ожидание (вывод), дисперсия, среднее квадратическое отклонение показательного распределения. Мат ожид- среднее значение случ величины,(M(x)=W_i X _iP_i)Мат ожид не явл полнлй хар-й ДСВ и поэт вводят D(х)

Дисперсие (M(X-(X)²) -наз мат ожид от квадрата отклонения случайной величины от своего мат ожид-я(средн знач квадр отклон). Недост диспер явл ее размерность которая равна квадрату разм-и Х.Поэт вводят Рабоч форм для диспер D(x)=М(х²)-М²(х)

41.Связь между показательным распределением и ПППС (доказательство теоремы).

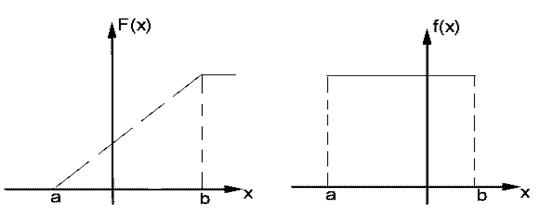
НСВ (х) имеет равномер распред если ф-я плотности имеет вид f(x)=1) 0, tckb x \э(a,b) 2)1/b-a, если x э(a,b) Имеет график: 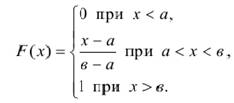-эта ф-я распр для равном закона.Имеет вид графика F(x): Вероят попад задан интервал для равном распред

42. Равномерное распределение, функция плотности, ее график случайная величина имеет равномерное распределение на отрезке [a,b], если она непрерывна, принимает значения только на отрезке [a,b], а плотность ее распределения постоянна на отрезке [a,b], и равна 0 вне этого отрезка. плотности (привязан к левой вертикальной оси ординат) и функции (привязан к правой оси ординат) равномерного распределения на отрезке [0,2].

Характеристики

Плотность распределения
Функция распределения
Математическое ожидание	(a + b) / 2
Дисперсия	(b - a)2 / 12

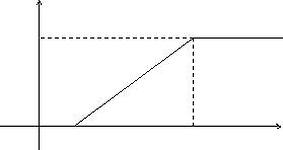
43. Функция распределения вероятностей равномерного распределения (вывод), ее график. Функция распределения имеет вид: график:

44. Математическое ожидание (вывод), дисперсия, среднее квадратическое отклонение равномерного распределения. 1. Математическое ожидание по формул 2. Дисперсия по формуле 3.среднее квадратическое отклонение – s(Х) по формуле