.Элементы\комбинаторики(перестановки,сочетания, размещения). Рассмотрим некоторое множество Х, состоящее из n элементов . Будем выбирать из этого множества различные упорядоченные подмножества Y из k элементов.Размещением из n элементов множества Х по k элементам назовем любой упорядоченный набор элементов множества Х.Если выбор элементов множества Y из Х происходит с возвращением, т.е. каждый элемент множества Х может быть выбран несколько раз, то число размещений из n по k находится по формуле (размещения с повторениями).Если же выбор делается без возвращения, т.е. каждый элемент множества Х можно выбирать только один раз, то количество размещений из n по k обозначается и определяется равенством Частный случай размещения при n=k называется перестановкой из n элементов. Число всех перестановок из n элементов равно . Пусть теперь из множества Х выбирается неупорядоченное подмножество Y (порядок элементов в подмножестве не имеет значения). Сочетаниями из n элементов по k называются подмножества из k элементов, отличающиеся друг от друга хотя бы одним элементом. Общее число всех сочетаний из n по k обозначается и равно .

2.Что называется испытанием, событием? Примеры Испытание-это выполнение соответст-ее некот условий.Событие-это результата испытания НР-Р: S”это испытание”:посадили 5 саженцев. А-прижились 5 саженцев В-приж-сь не менее 4 саж-в(4 или5) С-не прижилось ни один саженец(0 приж-сь) Д-приж-ся хотя бы один саженец(1 2 3 4 5)

3.Три вида событий (невозможные, достоверные, случайные). Определения и примеры. Событие-это результата испытания Испытание-это выполнение соответст-ее некот условий.3 вида событий: ДОСТОВЕРН_соответ-я кот-е при S испыт обязат произойдет.НР-Р :S: в урне 5 бел шаров.Наудачу достают 1 шар.А-шар бел, А и есть достов событие. НЕВОЗМОЖ-при S заведомо не произойдет НР-Р:S:в урне 5 б.ш Наудачу 1 шар.В-шар черн. В-невозм событие .СЛУЧАЙНЫЕ-при S могут произ или не мог произ-и.НР-Р: S: в урне 5б+3ч Наудачу берут 1 шар. А-шар б. А-случ событие.

4.Виды случайных событий Определения и примеры. 1)Событие А и В наз НЕСОВМЕСТ-ми если в рез одного испыт они появится не могут. ПР-Р: Монету подбрасывают 1 раз. А-выпал герб В- выпала решка. А и В- несовм-е. Событ А и В наз СОВМЕСТ-МИ если в рез испытания они могут появ вместе ПР-Р: S:посад 2 саженца А-приж-сь 2 саженца В-приж-сь не менее 1 саж-ца (1 2) . А и В-совмес события.2)Событие А1А2…Аn образ полную группу по парно несовместных событий если в рез испыт наступит одно из этих событий.Событие А1 А2 образуют полную группу группу событий если в рез обязат происходит одно из этих событий. ПР-р: S-посад 5 саж-в

А-ни 1 саж не приж В-хотя бы 1 саженец приж-ся. А и В образ полную группу несовм событий.3)ПРОТИВОП соб-события А и А/ наз против если выпол 2 услов 1)если они несовм 2) они полная группа событий 4) Событие называется невозможным, если оно никогда не произойдет в результате опыта.Например, если из коробки, содержащей только красные и зеленые шары, наугад вынимают один шар, то появление среди вынутых шаров белого – невозможное событие. События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью

5.Классическое определение вероятности события. Основное свойство вероятности 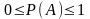(доказать).ПР-Р: В урне 5б+3ч ш.Наудачу берут 1 шар. А-ш бел В-шар чер. Для колич-ой оценки шансов наступления события вводят вероятность P(А) по формуле: P(А)=m/n-классич опред-е вероятностей события. N- общ число =возмож-х исходов m-число исходов благопр-х событию А. Получается: P(A)=m/n=5\8=0.625 ОСНОВ СВ-О ВЕРОЯТ-ТИ: 0≤ m≤n :n

0/n ≤m/n≤n/n

0≤P(A) ≤1 если событие невозможное…отс след P(V)=0 U-достов-е…p(u)=1 А-случ… 0<P(A)<1

6.Недостатки классического определения вероятности события. Статистическое и геометрическое определение вероятности события. Недостаток классического определения – он не приемним к испытаниям с бесконечным числом исходов Статистической вероятностью события А называется относительная частота появления этого события в произведенных испытаниях, т. е

Геометрическое определение вероятности. Пусть в некоторую область случайным образом бросается точка T, причем все точки области W равноправны в отношении попадания точки T. Тогда за вероятность попадания точки T в область A принимается отношение

, (где S(A) и S(W) — геометрические меры (длина, площадь, объем и т.д.) областей A и W соответственно

7.Связь и различие между классическим и статистическим определениями вероятности события. Вероятность – численная характеристика реальности появления того или

иного события.

Классическое определение вероятности: если множество возможных исходов

конечное число, то вероятностью события Е считается отношение числа исходов

благоприятствующих этому событию к общему числу единственновозможных равновозможных исходов. Классическое определение вероятности связано с непосредственным подсчетом

вероятности, требует точного знания числа всех возможных исходов, и удобно

для расчета вероятности достаточно простых событий.

Расчет вероятности более сложных событий - это сложная задача, требующая

определения чисел всех возможных комбинаций появления этих событий. Подобными

расчетами занимается специальная наука – комбинаторика. Поэтому на практике часто используется статистическое опред вероятн. Достоинство статистического определения вероятности в том, что для ее расчета не обязательно знать конечное число исходов.Если классическое определение вероятности осуществляется априори (до опыта), то статистическое апосториори (после опыта по результатам).Распределение частостей дискретного ряда, выраженных конечными числами, называется дискретным распределением вероятности. Если осуществляются исследования массовых событий частостей, которые распределяются непрерывно и могут быть выражены какой-либо функцией, называются непрерывным распределением вероятности.

8.Произведение событий. Вероятность произведения событий (вывод).

Над событиями можно производить 2 действия:умнож и склад

А *В- произ-е событий(произошло и А и В)

А ) А*В б)А*В=несовм соб

Вероят-ть произ-я событий. P(A*B)= P(A)*P(B),если А и В незав

=P(A)*P_a(B),если А и В-завис

P_a(B)-условн вероят-ть,рассчит при предположении что А произойдет.

9.Сумма событий. Вероятность суммы (вывод).(А+В)-сумма событий.Это означ что произойдет хотя бы 1 из событий А и В

P(A+B)=P(A)+ P(B),если А и В несовм

=P(A)+P(B)-P(A*B),еслт А и В совмест

10.Вероятность противоположного события (вывод).

А+А\=U(достоверн событие) P(A+A)они несовм=P(U) P(A)+P(A\)=1 Сумма вероятностей противополож событий=1

P(A)=P P(A\)=g p+g=1 =g=1-p-вероятн противоп события.

11. Вероятность появления хотя бы одного события

Вероятность появления события А заключающееся в наступлении хотя бы одного из

независимых совокупностей событий .А₁,А₂.А_n

равна разности между единицей и произведением вероятности противоположных

событий А₁,А₂.А_n

Р(А)=1-q¹*q²*.*qⁿ

12. Полная вероятность - постановка задачи и вывод формулы.

Рассмотрим события Н1, Н2,...,Нn, которые образуют полную группу попарно несовместных событий.

событие А может наступить одновременно с одним из Нj, поскольку неизвестно какое из Нj произойдет.

Hj называют гипотезами.

Событие А можно представить в виде: А=Н1*А+Н2*А+...+Нn*А

Вывод формулы: Р(А)=р(Н1*А)+р(Н2*А)+...+р(Нn*А)=р(Н1)*р(А)+р(Н2)*р(А)+...+р(Рn)*р(А)

Р(А)=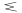 р(Нj)*р_Нj(А)

13. Переоценка вероятности гипотез- формулы Байеса.

Формулы Байеса позволяют провести переоценку вероятностей гипотез при условии, что событие А-уже произошло.

Р_А(Нj)=р(Нj)*р_Нj(А)/р(А)

14. Повторные независимые испытания. Формула Бернулли.

Введем обозначения: n-число, проведенных независимых испытаний.

p- вероятность наступления события А в каждом испытании.

q=(1-р) - вероятность ненаступления события А в каждом испытании.

k - число наступления события А в n испытаниях.

P_n(k)=C^k_n*p^k*q^n-k - формула Бернулли.

15. Приближенные формулы Муавра-Лапласа(локальная и интегральная). Свойства и графики функций Гаусса и Лапласа.

Локальная формула Муавра-Лапласа.

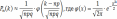
График функции Гаусса имеет вид "шапочки".

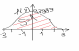
Свойства функции Гаусса:

1) фи(х)-четная ф-я.

фи(-х)=фи(х)

2) фи_max=фи(0)=1/√2пи

3) при х>4 фи(х)≈0

Интегральная формула Муавра-Лапласа.

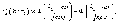где

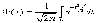
Свойства ф-ии Ф(х): 1)Ф(-х)=-Ф(х)=>Ф(х)-нечетн.

2) при х>5 Ф(х)≈0,5

3) Ф(0)=0

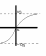
16. Формула Пуассона для многочисленных, но редких испытаний.

n- очень велико (n≥100)

p-очень мало (p≤0,1)

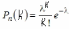
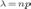
17. Простейший Пуассоновский поток событий.

Пуассоновским потоком называют ординарный поток заявок с отсутствием последействия, у которых количество заявок, поступающих в систему за промежуток времени t распределено по закону Пуассона:

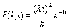
, t>0, λ>0 (*)

где Р(k,t) - вероятность того, что за время t в систему поступит ровно k заявок

λ -среднее число событий в единицу времени( интенсивность потока)

Математическое ожидание и дисперсия для закона Пуассона:

М[T]=D[T]=λ*t