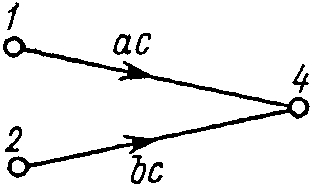
5) Способы задания и преобразования ориентированных графов

Способы задания:

Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера [n x n], в которой значение элемента a_ij равно числу рёбер из i-й вершины графа в j-ю вершину.

Матрица инцидентности — одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина). Столбцы матрицы соответствуют ребрам, строки — вершинам.

D = <V,E>

Если e_i является петлей при вершине v_j , то элемент w_i,j равен любому числу, отличному от 1, -1 и 0.

Матрица смежности неориентированного графа симметрично относительно главной диагонали. Матрица ориентированного графа - не симметрична.

Способы преобразования:

№ п/п	Исходный граф	Преобразованный граф	Характер преобразований
1			Передача последовательных ветвей
2			Передача параллельных ветвей
3			Исключение простого узла
4			Исключение простого узла
5			Исключение петли

6) Способы задания и преобразования неориентированных графов. Матричное задание графов:

Способы задания:

1. Аналитический способ задания. Граф задаётся с помощью формул в виде G = (X,Y). Этот способ мало информативен и носит академический характер. Подобное представление бывает полезным приформальных описаниях графа при решении математических задач.

2. Задание графа с помощью рисунка. Способ очень наглядный, даёт максимум информации, однако имеет существенный недостаток: плохо формализован, поэтому неудобен для формальной реализации алгоритмов решения задач топологического проектирования.

3. Матричное задание графа. Этот способ менее нагляден, чем предыдущий, однако несёт всю информацию о графе, хорошо формализован и используется во всех алгоритмах как основной. Матричный способ задания графов представляется в виде двух основных типов матриц: матрицы смежности и матрицы инцидентности

Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера [n x n], в которой значение элемента a_ij равно числу рёбер из i-й вершины графа в j-ю вершину.

Матрица инцидентности — одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина). Столбцы матрицы соответствуют ребрам, строки — вершинам.

7) Действия над неориентированными графами

Объединением графов  и   называется граф , множество вершин которого есть объединение множеств вершин графов  и , а множество ребер является объединением множеств ребер  этих графов .

Пересечением графов  и  называется граф , множество вершин которого , а множество ребер .

Кольцевой суммой графов  и  называется граф , порожденный на множестве ребер , т. е. на множестве ребер, присутствующих либо в , либо в , но не принадлежащих их пересечению

Вычитание графов условно записывают следующим об­разом:

С(х, l) = G₁(X_i, Г,)\С,(Х_г, Г,), где G(X, Г) — граф, полученный в результате вычитания исходных графов G,(X_lf Г,) и G₂{X₂, Г₂).