4.18. В чем сущность метода итерации для решения слау, как еще называют этот метод.

Метод простых итераций или метод Якоби

Рассмотрим неоднородную систему линейных алгебраических уравнений (СЛАУ)

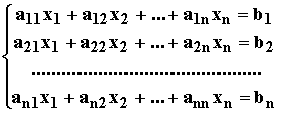(1)

Для получения итерационных формул метода простых итераций из первого уравнений СЛАУ (3.6) выражается x₁, из второго – x₂, из последнего n-го уравнения – x_n. В результате получим систему

x₁= (b₁- a₁₂x₂ - a₁₃x₃ - … - a_1n x_n) / a₁₁;

x₂ = (b₂– a₂₁x₁ – a₂₃x₃ - … - a_2n x_n) / a₂₂;

………………………………………….

x_n = (b_n– a_n1x₁ – a_n2x₂ - … - a_{n n-1} x_n-1) / a_nn.

Или в общем виде

, i=1, n

k=1,2, …до тех пор пока

x(k)-x(k-1) .

Достаточным условием сходимости решения системы (1) является диагональное преобладание матрицы A:

.

На каждом шаге происходит приближение корней СЛАУ к истинным значениям.

4.19	Сформулируйте достаточные условия сходимости метода Зейделя для решения СЛАУ.

Обычно процесс Зейделя сходится быстрее, чем метод Якоби. Бывает, что процесс Зейделя сходится, когда простая итерация расходится и, т.п. Правда, бывает и наоборот. Во всяком случае, достаточные условия сходимости для метода Якоби достаточны и для сходимости метода Зейделя. Если выполняется достаточное условие сходимости для системы 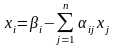(i = 1, 2, …n).

– по строкам, то в методе Зейделя выгодно расположить уравнения

так, чтобы первое уравнение системы имело наименьшую сумму модулей коэффициентов:

.

Достаточным условием сходимости решения системы A·x = f, является то, что матрица A является матрицей с преобладающими диагональными элементами, то есть

4.20	Назовите особенности метода Зейделя.

Является модификацией метода Якоби и отличается от него, тем, что для вычисления корня, на к+1 итерации используются корни в формуле Якоби уже вычисленное на этой, к+1 итерации.

Сходимость метода Зейделя выше, чем в методе Якоби, однако существуют СЛАУ, для которых метод Якоби сходится, а метод Зейделя расходится. В этом случае существует собственное условие сходимости Зейделя определяет.

Т: Пусть А вещественная положительная определенная матрица, тогда метод Зейделя сходится при любых начальных приближениях.

4.21	Назовите функции для решения систем уравнений в Mathcad и особенности их применения.

Для решения СЛАУ в ППП MathCad используется процедура lsolve. Рассмотрим применение процедуры на следующим примере:

Решением этой система являются значения х₁=3,  х₂=2.

В пакете Mathcad найти решение этой системы можно так:

.

Отметим, что задав матрицу A и вектор b вектор неизвестных x можно найти решив непосредственно векторно-матричное уравнение

.

4.22	Метод Зейделя для решения СЛАУ

Метод Зейделя

Этот метод представляет собой некоторую модификацию метода простой итерации. Основная его идея заключается в том, что при вычислении (k+1)-го приближения неизвестной x_i учитываются уже вычисленные ранее (k+1)-е приближения (x₁ x₂, ..., x_i-1).

Пусть дана приведенная линейная система:

(i = 1, 2, …n). (1)

Выберем произвольно начальные приближения корней , стараясь, конечно, чтобы они в какой-то мере соответствовали неизвестным x₁, x₂, x₃, ..., x_n.

Предположим, что k-е приближение корней известно, тогда в соответствии с идеей метода будем строить (k+1) – е приближение по следующим формулам:

(2)

(k = 0, 1, 2,...).

Обычно процесс Зейделя сходится быстрее, чем метод Якоби. Бывает, что процесс Зейделя сходится, когда простая итерация расходится и, т.п. Правда, бывает и наоборот. Во всяком случае, достаточные условия сходимости для метода Якоби достаточны и для сходимости метода Зейделя. Если выполняется достаточное условие сходимости для системы (1) – по строкам, то в методе Зейделя выгодно расположить уравнения (2) так, чтобы первое уравнение системы имело наименьшую сумму модулей коэффициентов:

. (3)

4.23	Основная идея метода Гаусса с выбором главного элемента

1. На каждом шаге преобразования выбирается максимальный по модулю элемент а_pq, р-ая строка главная а_pq-главный

2. для всех строк, кроме главной находится сомножитель

3. Каждой неглавной строке добавляем главную умножающую на сомножитель m_i, в результате q-ый столб нулевой, вычеркиваем p-ую строку и q-ый столбец

4. Повторяем процедуру (n-1) раз

5. Составляем матрицу из вычеркнутых строк, она не треугольного вида, однако строка последнего преобразования содержит только один элемент, предпоследнего 2-а и т.д. в этом порядке и вычисляем неизвестное х_i

4.24	Вычисление обратной матрицы по методу Гаусса

Вычисление обратной матрицы методом Гаусса

Пусть дана неособенная матрица

A = [a_ij] (i,j = 1,2, ..., n).

Необходимо найти её обратную матрицу

A^-1 = [x_ij] (i,j = 1,2, ..., n).

Вспомним основное соотношение линейной алгебры:

A·A^-1 = E,

где Е – единичная матрица.

Перемножая матрицы A и A^-1, получаем n² уравнений относительно n² неизвестных x_ij:

(i,j = 1, 2, ..., n),

где

Таким образом, получим n систем линейных уравнений для j = 1, 2, ..., n, имеющих одну и ту же матрицу коэффициентов A и различные столбцы - свободные члены, которые можно одновременно решить методом Гаусса.

4.25	Основные классы методов решения СЛАУ

Методы решения СЛАУ

Разделяют на две группы:

1) прямые

2) итерационные

1. Прямые позволяют получить решение за конечное число шагов (достоинство метода), не накапливают ошибки вычисления

недостатки: 1) применимы лишь к матрицам ограниченной размерности (200)

2) требуют хранения всей матрицы системы, на каждом шаге

3) плохо работают с разряженными (неплотными (много нулей)) матрицами

к ним относятся: метод Гаусса, Крамера, Жордан, метод главных компонентов.

2. итерационны

недостатки: 1) нельзя заранее определить количество шагов (итераций)

2) методы накапливают погрешность

достоинства: 1) применимы к системам любой размерности

2) работают со слабо заполненными матрицами

относятся: 1) метод простых итераций (Якоби)

2) Зейделя

3) Релаксации

4.26	Вычисление определителя по методу Гаусса