4.10 Нормой матрицы l называют такое вещественное число, которое удовлетворяет следующим условиям:

5. ||α||=0 тогда и только тогда, когда Lij=0

6. ||α*a||=|a|*||α||

7. ||α*B||=||α||*||B||

8. ||α+B||=||α||+||B||

4.11 Примеры норм матриц

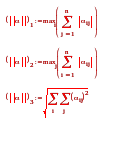
4.12	Укажите условия сходимости метода Якоби для решения СЛАУ

Для того, чтобы метод простых итераций (Якоби) сходился при любом начальном векторе необходимо чтобы какая-либо норма матрицы α<1 (||α||<1)

Нормой матрицы α называют такое вещественное число, которое удовлетворяет следующим аксиомам.

1) ||α||=0 => α_ij=0

2) ||λα||=|λ|*||α||

3) ||αβ||≤||α||*||β||

4) ||α+β||≤||α||+||β||

α,β – матрицы, λ-const

Достаточным условием сходимости решения системы A·x = f, является то, что матрица A является матрицей с преобладающими диагональными элементами, то есть

4.13	Методика приведения СЛАУ к сходящемуся виду

Для приведения матрицы А к сходящемуся виду практически поступают следующим образом:

1. Из заданной системы выделяют уравнения, модули коэффициентов которых больше суммы модулей остальных коэффициентов в виде этих уравнениях.

2. Каждое из выделенных уравнений записывается в такую строку новой системы, чтобы этот максимальный элемент стал диагональным.

3. Из оставшихся и выделенных уравнений системы составляются линейно независимые между собой линейные комбинации так, чтобы выполнялся принцип 2., были заполнены все свободные строки новой системы и были использованы все уравнения исходной системы.

4.14	Дайте сравнительную оценку методам решения СЛАУ.

Существуют 3 основных метода решения СЛАУ: метод Гаусса, метод Якоби и метод Зейделя.

Метод Гаусса является прямым методом решения СЛАУ. Это значит, что в отличие от методов Якоби и Зейделя он не накапливает ошибок вычислений, но применим только к матрицам ограниченной размерности, и плохо работает с разряженными матрицами.

Метод Зейделя в отличие от метода Якоби позволяет достичь требуемых значений погрешности за меньшее количество итераций, следовательно он более эффективен, чем метод Якоби.

Метод Гаусса лучше работает не разреженными матрицами ограниченной размерности, в противном случае более эффективен метод Зейделя.

4.15	Чем точные методы решения СЛАУ отличаются от приближенных?

Применяемые в настоящее время методы решения СЛАУ можно разбить на две группы: точные и приближённые.

Точными методами называются такие методы, которые в предположении, что вычисления ведутся точно (без округлений), за конечное число действий позволяют получить точные значения неизвестных x_i.

Приближенными методами называются такие методы, которые даже в предположении, что вычисления ведутся без округлений, позволяют получить решение системы (x₁, x₂, ..., x_n) лишь с заданной точностью. Точное решение СЛАУ в этих случаях может быть получено теоретически как результат бесконечного процесса.

К приближенным методам относятся метод простой итерации, метод Зейделя и т.п.я матрицы А к сходящимуся

4.16	В каких случаях целесообразно использовать итерационные методы решения СЛАУ?

Не итерационные методы способны считать СЛАУ с определенной точностью. Если нам нужно посчитать с другой точностью, той которая необходима нам, нужно использовать итерационные методы. В итерационных методах мы сами задаем точность.

4.17 Что влияет на скорость сходимости итерационного процесса

На скорость сходимости итерационного процесса влияет: входные данные, т.е. вектор начальных приближений, выбранный метод вычислений.