
- •1.1 Что такое погрешности числа и вычислений.
- •1.2. Дайте определение погрешности.
- •1.4. Укажите формы записи абсолютной погрешности.
- •1.14. Привести формы записи числа с фиксированной и плавающей запятой. Привести примеры записи.
- •1.15. Что такое сомнительные и верные числа числа. Способы их вычисления.
- •1.24. Понятие вычислительного эксперимента.
- •1.27. Сколько значащих цифр в числе 1223.0034
- •1.28. Как влияет способ представления чисел в эвм на точность результатов.
- •3.1. Назовите приближенные методы решения систем нелинейных уравнений
- •3.6.Основные понятия итерационного процесса
- •3.20.Правило останова итерационных методов решения нелинейных уравнений
- •Метод простых итераций (метод Якоби) для решения систем нелинейных уравнений
- •Метод Ньютона для решения систем нелинейных уравнений
- •4.10 Нормой матрицы l называют такое вещественное число, которое удовлетворяет следующим условиям:
- •4.11 Примеры норм матриц
- •4.18. В чем сущность метода итерации для решения слау, как еще называют этот метод.
- •Метод Зейделя
- •Вычисление определителей методом Гаусса
- •5.1 Обыкновенное дифференциальное уравнение и уравнение в частных производных
- •5.2 Задача Коши и краевая задача
- •5.3 Методы Рунге-Кутта
- •5.7 Решение систем дифференциальных уравнений
- •5.8 Дайте определение задачи Коши
- •5.9 Дайте определение краевой задачи
- •5.10 Приведите классификацию дифференциальных уравнений
- •5.20 Методы Рунге для решении задачи Коши (идея и особенности)
- •5.21 Метод Эйлера для решения задачи Коши
- •5.22 Принцип Рунге для оценки шага при решении задачи Коши
- •5.23 Источники погрешности методов Рунге - Кутта
- •6.1 Основные задачи аппроксимации функций
- •6.2 Понятие интерполяции данных, критерий интерполяции
- •6.4 Фильтрация и сглаживание данных
- •6.5 Регрессионное уравнение
- •6.6 Метод наименьших квадратов
- •6.7 Экстраполяция данных (прогноз данных)
- •6.8 Показатели эффективности аппроксимации
- •6.9 Решение задач аппроксимации в пакете MathCad
- •6.10 Приведите понятие аппроксимации функций
- •6.11 Приведите понятие интерполирования данных (глобальная и локальная интерполяция)
- •6.12 Что такое сглаживание данных
- •6.17 В чем состоит основная идея сплайн аппроксимации.
- •6.18 Критерий метода наименьших квадратов
- •6.20. Процедуры интерполирования данных в ппп MathCad
- •6.21 Понятие регрессионного уравнения
- •6.22 Что такое базисные функции? Пример базисных функций.
- •6.23 Суть метода наименьших квадратов
- •6.24 Понятие аппроксимации
- •6.25. Показатели эффективности приближения данных
Метод Ньютона для решения систем нелинейных уравнений
Этот метод обладает более быстрой сходимостью, чем метод простой итерации. Рассмотрим реализацию метода Ньютона для системы из двух нелинейных уравнений вида (3.14).
При итерационном нахождении корней каждое последующее значение отличается от предыдущего на некоторую величину . Запишем формально итерационные формулы для двух корней
(3.20)
Разложим левые части нелинейных уравнений (4.14) в ряд Тейлора в окрестности точки (x1k, x2k) и ограничимся производными первыми порядка. Получим

Пусть приращения xik, i=1,2 таковы, что функции f1, f2 принимают значения близкие к корню, т.е. левые части предыдущей системы равны нулю. Перепишем систему с учетом этого

Или в векторно- матричной форме
 (3.21)
(3.21)
В сокращенной форме
 (3.22)
(3.22)
Здесь
 - матрица частных производных Якоби,
вычисленная для приближенных корней
xik, i=1,2.
- матрица частных производных Якоби,
вычисленная для приближенных корней
xik, i=1,2.
Неизвестными в этой системе являются приращения xik, i=1,2. Разрешим систему (3.22) относительно xik
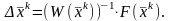
Найденные приращения используются как поправка к корню, полученному на предыдущем шаге xik, i=1,2. Подставим поправки в формулу (3.20) получим окончательно формулу Ньютона
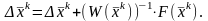 (3.23)
(3.23)
Если систему двух уравнений (3.21) разрешить относительно приращений не в матричной форме, а например, по правилу Крамера, то получим выражения для приращений в виде
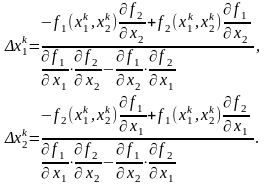
Эти приращения затем используются в формуле (3.20) для нахождения приближения к корням системы на новом шаге.
Замечания.
1. Окончание итерационного процесса возможно либо по стандартному условию останова (3.20), либо когда все приращения xik, i=1,2 стремятся к нулю. т.е.
 . (3.24)
. (3.24)
Правило останова (3.24) означает, что найденные на данной итерации приращения практически не изменяются, т.е. корни уравнения найдены с заданной точностью.
2. Метод Ньютона обеспечивает более быструю сходимость, чем метод простых итераций. Особенно его эффективность заметна при удачном выборе начальных приближений. Сходимость ухудшается с увеличением числа уравнений.
3.25 |
Метод дихотомии для решения нелинейных уравнений |
Ш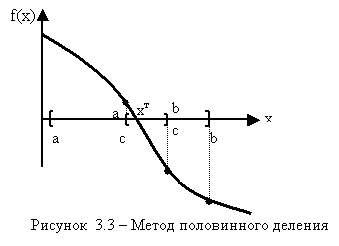 аг
1. Выбор
интервала [a, b], такого что f(a)f(b)<0.
Задание точности вычисления корня .
Счетчик числа итераций n=0.
аг
1. Выбор
интервала [a, b], такого что f(a)f(b)<0.
Задание точности вычисления корня .
Счетчик числа итераций n=0.
Шаг 2. Вычисление c=(a+b)/2, n=n+1.
Шаг 3. Если f(a)f(c)<0,то b=c, иначе a=c.
Шаг 4. Если b-a> , то переход на Шаг 2, иначе выход из итерационной процедуры, печать результатов: корень уравнения c, число итераций n.
3.26 |
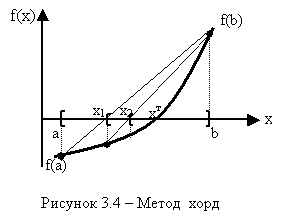
Метод хорд для решения нелинейных уравнений |
Метод также относится к интервальным, т.е. требует первоначального выбора интервала [a, b]. Алгоритмизация метода практически совпадает с методом половинного деления, за исключением шага 2.
Шаг 1. Выбор интервала [a, b], такого что f(a)f(b)<0. Задание точности вычисления корня . Счетчик числа итераций n=0.
Шаг 2. Вычисление c=(a+b)/2, n=n+1.
Шаг 3. Если f(a)f(c)<0,то b=c, иначе a=c.
Шаг 4. Если b-a> , то переход на Шаг 2, иначе выход из итерационной процедуры, печать результатов: корень уравнения c, число итераций n.
Вместо деления интервала [a, b] пополам метод предполагает поделить его в отношении f(a) / f(b). Графически это означает построение хорды между точками f(a) и f(b). Уравнение этой прямой имеет вид
![]() .
.
Эта прямая пересекает ось OX при значении x=c, f (c)=0. Отсюда найдем искомое приближение к корню xт :
|
(3.14) |
В остальном алгоритмизация метода хорд полностью повторяет предыдущую.
Замечание:. В некоторых случаях (как, например, на рис.3.4.) стандартное правило останова итерационной процедуры b-a<, может не привести к решению, т.к. одна из границ остается неподвижной. В этом случае целесообразно использовать следующее правило останова
|
(3.15) |
где xn, xn-1 значения корней на двух соседних итерациях, найденные по формуле (3.14).
3.27 |
Метод касательных (Ньютона) для решения нелинейных уравнений |
о чень
популярен. Это объясняется тем, что в
отличии от методов дихотомии и хорд,
метод ньютона не требует первоначального
задания интервала, на концах которого
функция имеет разные знаки. Вместо
интерполяции по двум точкам, в методе
Ньютона осуществляется экстраполяция
(прогнозирование) с помощью касательной
к функции.
чень
популярен. Это объясняется тем, что в
отличии от методов дихотомии и хорд,
метод ньютона не требует первоначального
задания интервала, на концах которого
функция имеет разные знаки. Вместо
интерполяции по двум точкам, в методе
Ньютона осуществляется экстраполяция
(прогнозирование) с помощью касательной
к функции.
Для начала работы метода требуется найти точку х0, в которой выполняется следующее условие
![]() ,
,
т.е. функция и ее вторая производные в этой точке были одного знака (как правило концы интервала [a,b].
Корень нелинейного уравнения уточняется по соотношению
|
(3.16) |
Правило останова
. |
(3.15) |
3.28 |
Метод простых итераций для решения нелинейных уравнений |
Основная идея метода заключается в разделении нелинейного уравнения f(x)=0 не линейную и нелинейную части: x=f1(x)
Тогда
имея начальное приближение x0,
получаем итерационную процедуру :
 ,
,
где f1(x) – нелинейная часть функции f(x)
Успех метода простых итераций определяется верным выделением нелинейной части.
3.29 |
Опишите основные свойства прямых и итерационных методов решения уравнений. |
Прямые методы позволяют найти корни только для отдельных нелинейных равнений (алгебраических 2-го порядка, неполных логарифмических и т.д.). В общем случае решать уравнения прямыми методами невозможно.
Особенности итерационных методов:
1)Решение
осуществляется по одной и той же
повторяющейся формуле f:
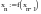
2)Для реализации итерационных процедур необходимо начальное значение x
3)Необходимая
точность вычисления корня и условие
останова итерационного процесса:
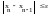
4)Важнейшей характеристикой любого итерационного метода является количество шагов n и связанное с ним быстродействие метода
5)Скорость сходимости r
3.30 |
Что понимают под сходимостью итерационной процедуры. Примеры. |
В итерационных методах решения получают, исходя из начального решения x0, получив последовательность решений x0,x1,x2,…,xn. Если эта последовательность сходится к точному x при n стремящемся к бесконечности, то метод называется сходящимся.
3.31 |
Поясните, что такое скорость сходимости и как она связана с эффективностью метода.
|
 ,
x^T
– x точное
,
x^T
– x точное
r=1 – линейная сходимость
r=2 – квадратичная сходимость (иногда)
r=3 – редко и т.д.
Чем больше скорость сходимости, тем эффективнее метод
4.1 |
Основные задачи линейной алгебры |
|
4.2 |
Прямые и итерационные методы решения СЛАУ |
|
4.3 |
Метод исключения Гаусса |
|
4.4 |
Задачи, сопутствующие реализации метода Гаусса |
|
4.5 |
Итерационные методы решения СЛАУ |
|
4.6 |
Достаточные условия сходимость итерационных методов решения СЛАУ |
|
4.7 |
Метод Якоби для решения СЛАУ |
|
4.8 |
Решение задач линейной алгебры в ППП MathCad |
|
4.9 |
Приведите достаточные условия сходимости метода Якоби (теорема) для решения СЛАУ |
|
4.10 |
Дайте определение нормы матрицы 504 |
|
4.11 |
Приведите примеры норм матриц |
|
4.12 |
Укажите условия сходимости метода Якоби для решения СЛАУ |
|
4.13 |
Методика приведения СЛАУ к сходящемуся виду |
|
4.14 |
Дайте сравнительную оценку методам решения СЛАУ. |
|
4.15 |
Чем точные методы решения СЛАУ отличаются от приближенных? |
|
4.16 |
В каких случаях целесообразно использовать итерационные методы решения СЛАУ? |
|
4.17 |
Что влияет на скорость сходимости итерационного процесса? |
|
4.18 |
В чем сущность метода итерации для решения СЛАУ, как еще называют этот метод? |
|
4.19 |
Сформулируйте достаточные условия сходимости метода Зейделя для решения СЛАУ. |
|
4.20 |
Назовите особенности метода Зейделя. |
|
4.21 |
Назовите функции для решения систем уравнений в Mathcad и особенности их применения. |
|
4.22 |
Метод Зейделя для решения СЛАУ |
|
4.23 |
Основная идея метода Гаусса с выбором главного элемента |
|
4.24 |
Вычисление обратной матрицы по методу Гаусса |
|
4.25 |
Основные классы методов решения СЛАУ |
|
4.26 |
Вычисление определителя по методу Гаусса |
|
4.27 |
Как организовать контроль прямого хода метода Гаусса |
|
4.28 |
Как организовать контроль обратного хода метода Гаусса |
|
4.1 |
Основные задачи линейной алгебры |
Раздел математики, занимающийся изучением линейных уравнений и систем линейных уравнения, называется линейной алгеброй.
Основные задачи:
1)Решение СЛАУ;
2)Вычисление определителя фундаментальной матрицы;
3)Нахождение обратной матрицы;
4)Вычисление собственных значений и собственных векторов.
4.2 |
Прямые и итерационные методы решения СЛАУ |
Прямые (метод Гаусса)
+ Позволяют получить решение за конечное число шагов
+ Не накапливают ошибки вычислений
- Применимы лишь к матрицам ограниченной размерности
- Требует хранения всей матрицы решения на каждом шаге
- Плохо работает с разряженными (неплотными) матрицами
Итерационные (Метод Якоби)
+ Применимы к системам любой размерности
+ Работает со слабо заполненными матрицами
- Нельзя заранее определить количество шагов
- Методы накапливают погрешность
4.3 |
Метод исключения Гаусса |
Основная идея – приведение матрица А к верхнетругольному виду. Для этого проводятся n линейных преобразований, в ходе которых вначале обнуляются все коэффициенты ниже а11, затем ниже а22 и т.д. В результате получаем матрицу верхнетреугольного вида, в последнем уравнении которой только 1 число при неизвестном xn. Корни вычисляем в обратном порядке, начиная с xn
I. Прямой ход. Приведение матрицы A к верхнетреугольному виду. Для этого выполняется n преобразований матрицы A. На каждом шаге преобразования выбирается главная k-ая строка. Диагональные элементы главной строки называются главными (ведущими). На прямом ходе выполняется следующее преобразование:
главную строку делим на главный элемент akk;
для остальных строк находим множитель lik;
к каждой неглавной добавляем главную, умноженную на множитель lik;
главную строку вычеркиваем, размерность системы становится (n-1).
На следующем шаге исключения главной строкой становится опять верхняя (под вычеркнутой). Преобразования повторяются до тех пока главная строка не становится единственной в системе. В результате – матрица A верхнетреугольного вида.
II.
Обратный ход. Вектор
неизвестных СЛАУ
![]() находится
в обратном порядке. Для этого составляется
матрица из вычеркнутых строк
верхнетреугольного вида. Из последнего
уравнения находится xn,
затем неизвестные находятся в порядке
xn-1,
xn-2,
..., x1.
находится
в обратном порядке. Для этого составляется
матрица из вычеркнутых строк
верхнетреугольного вида. Из последнего
уравнения находится xn,
затем неизвестные находятся в порядке
xn-1,
xn-2,
..., x1.
4.4 |
Задачи, сопутствующие реализации метода Гаусса |
Треугольная факторизация матриц.
В результате реализации метода Гаусса матрица системы А может быть представлена в виде произведения двух треугольных матриц L – нижнетреугольной и V - верхнетреугольной:
А=LV.
 ,
,
где элементы матриц получены по формулам (3.8).
Пример.
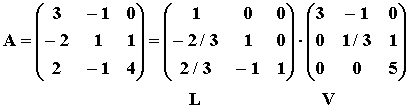
Вычисление определителей.
det A=det L det V =1 a11a22(1)… ann(n-1)
Пример. det A = 1 3 1/35 = 5
Вычисление обратной матрицы
основано на основном свойстве обратной матрицы A A-1 = Е,
где Е – единичная матрица. Запишем это уравнение в развернутом виде:

Т.о. нахождение обратной матрицы сводится к решению n систем СЛАУ, у которых одна общая матрица A, а столбцами свободных членов являются столбцы единичной матрицы E.
4.5 |
Итерационные методы решения СЛАУ |
При большом числе неизвестных линейной системы схема метода Гаусса и его модификации, дающие точное решение, становится сложной. В этих условиях для получения решения можно использовать итерационные методы. Решение в этих методах получается как предел последовательных приближений к решению x(0), x(1), … ,x (k)xт. Здесь xтточное решение системы. x(0), x(1), …вектора решений, полученные на 0, 1, … итерациях.
Для реализации итерационных методов необходимо:
Начальное приближение x(0).
Итерационная формула, определяющая приближение через предыдущее x(k) = (x(k-1)).
Точность и условие проверки на точность x(k)-x(k-1).
Считается, что решение найдено, если выполняется условие 3. и доказана сходимость последовательности векторов x(0), x(1), … ,x(k).
В зависимости от конкретного вида итерационной формулы существует несколько методов решения СЛАУ. Наиболее известные из них метод Якоби (простых итераций) и метод Зейделя.
4.6 |
Достаточные условия сходимость итерационных методов решения СЛАУ |
Достаточным условием сходимости решения СЛАУ является диагональное преобладание матрицы A:
|
(3.12) |
4.7 |
Метод Якоби для решения СЛАУ |
Для получения итерационных формул метода простых итераций из первого уравнений СЛАУ (3.6) выразим x1, из второго – x2, из последнего n-го уравнения – xn. В результате получим систему
x1= (b1- a12x2 - a13x3 - … - a1n xn) / a11;
x2 = (b2– a21x1 – a23x3 - … - a2n xn) / a22;
………………………………………….
xn = (bn– an1x1 – an2x2 - … - an n-1 xn-1) / ann.
Или в общем виде
|
(3.10) |
k=1,2, …до тех пор пока |
x(k)-x(k-1) . |
(3.11) |
Достаточным условием сходимости решения системы (3.6) является диагональное преобладание матрицы A:
. |
(3.12) |
Проверку сходимости по формуле (3.11) можно осуществлять суммированием либо по столбцам матрицы, либо – по строкам.
Для приведения матрицы A к сходящемуся виду практически поступают следующим образом:
Из заданной системы выделяют уравнения, модули коэффициентов которых больше суммы модулей остальных коэффициентов в этих уравнениях.
Каждое из выделенных уравнений записывается в такую строку новой системы, чтобы этот максимальный элемент стал диагональным.
Из оставшихся и выделенных уравнений системы составляются линейно независимые между собой линейные комбинации так, чтобы выполнялся принцип 2. , были заполнены все свободные строки новой системы и были использованы все уравнения исходной системы.
4.8 |
Решение задач линейной алгебры в ППП MathCad |
Для решения СЛАУ в ППП MathCad используется процедура lsolve. Рассмотрим применение процедуры на следующим примере:
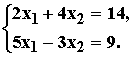
Решением этой система являются значения х1=3, х2=2.
В пакете Mathcad найти решение этой системы можно так:
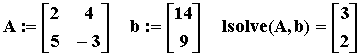 .
.
Отметим, что задав матрицу A и вектор b вектор неизвестных x можно найти решив непосредственно векторно-матричное уравнение
 .
.
4.9 |
Приведите достаточные условия сходимости метода Якоби (теорема) для решения СЛАУ |
Т: Для того, чтобы метод Якоби сходился при любом начальном векторе x0, необходимо чтобы какая-либо норма матрицы L была меньше 1.
Нормой матрицы L называют такое вещественное число, которое удовлетворяет следующим условиям:
||L||=0 тогда и только тогда, когда Lij=0
||L*a||=|a|*||L||
||L*B||=||L||*||B||
||L+B||=||L||+||B||

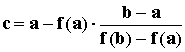 .
.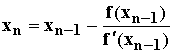
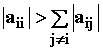 .
.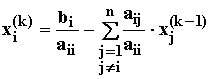 ,
i=1, n
,
i=1, n