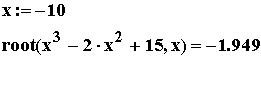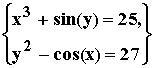3.20.Правило останова итерационных методов решения нелинейных уравнений

|b-a|<ε

|x_n-x_n-1|< ε

3.21	Условия сходимости метода простых итераций 507

Пусть функция f(x) определена и непрерывна на [a,b], тогда если 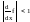, для любого x принадлежащего [a,b], то метод простых итераций с любой допустимой погрешностью за конечное число шагов.

3.22	Вычислительные (решающие) блоки ППП MathCad для решения нелинейных уравнений и систем нелинейных уравнений

Для решения нелинейных уравнений могут использованы следующие процедуры Mathcad:

• root;

• вычислительный блок Given - Find (Дано - Найти);

• вычислительный блок Given - Minerr (Дано - Минимальная погрешность).

Процедура root позволяет найти только один корень уравнения. Причем, перед использованием процедуры требуется задать начальное значение (приближение) корня. Синтаксис этой процедуры приведен ниже:

Для root процедуры большое значение имеет начальное приближение к корню. Например, если вместо х:=-10 , задать значение х:=10, то процедура root вообще не найдет корень и выдаст об этом сообщение. Особенности применение вычислительных блоков рассмотрим на примере решения  системы нелинейных уравнений:

 Продемонстрируем решение этой система в пакете Mathcad:

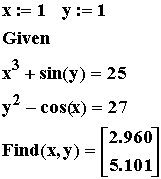
При использовании вычислительного блока необходимо учитывать следующие особенности:

1. Должны быть определены начальные приближения к корням (в данном примере x:=1 y:=1).

2. В равенствах должны быть использованы знаки тождественного равенства (жирное равенство с Палитры отношений и логики). Кроме равенств система может включать и неравенства, образуемые знаками < , > ,  , .

3. Служебные слова Given, Find могут быть взяты из служебных слов, либо просто напечатаны.

Вычислительный блок Given - Find создает итерационную последовательность приближений к корню, начиная с заданного начального приближения. Полученное решение таково, что при подстановке его в уравнения правая и левая часть его отличается на величину TOL (TOLerance - точность, погрешность). По умолчанию величина TOL =10^-3. Если требуется более точный результат, то величину TOL можно сменить либо в меню MATH  Options, либо задав величину в рабочем листе, например TOL :=10^-8. (Имя переменной TOL записывается только в верхнем регистре).

Правила записи вычислительного блока Given - Minerr такие же. Однако итерационная процедура поиска корней ориентирована на поиск решения, минимизирующего разность правой и левой части уравнений. Поэтому возможны ситуации, когда при одних и техже начальных приближениях вы числительные блоки Given - Minerr и Given - Find приводят к разным решениям.

3.23	Геометрическая интерпретация сходимости метода простых итераций

3.24	Методы решения систем нелинейных уравнений

Метод простых итераций (метод Якоби) для решения систем нелинейных уравнений

Метод Якоби, как и в одномерном случае, основан на предположении, что каждое нелинейное уравнение f₁(x₁,x₂) и f₂(x₁,x₂) системы (3.14) можно разделить на линейную(x) и нелинейную((x)) часть. Причем из первого уравнения линейно извлекаем x₁, а из второго – соответственно – x₂. Получим

(3.15)

Выбрав начальное приближение (x₁⁰, x₂⁰), подставим его в правую часть системы (3.15).

Проделав аналогичные операции для (x₁¹, x₂¹), (x₁², x₂²),…, (x₁^k-1, x₂^k-1), получим общую формулу метода простых итераций

(3.16)

По формуле (3.16) может быть организована итерационная процедура приближения к корню системы нелинейных уравнений. Итерационный процесс продолжается до тех пор, пока обе координаты корня (x₁^k, x₂^k) будут меняться существенно. Обрыв итерационного процесса осуществляется на основе правила останова, аналогичного одномерному случаю.

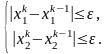(3.17)

Здесь  - точность вычисления корня.