3.1. Назовите приближенные методы решения систем нелинейных уравнений

Метод Якоби, Зейделя, Ньютона.

1) Метод Якоби основан на предположении, что каждое нелинейное уравнение f₁(x₁,x₂) и f₂(x₁,x₂) системы можно разделить на линейную(x) и нелинейную((x)) часть. Причем из первого уравнения линейно извлекаем x₁, а из второго – соответственно – x₂. Получим

Выбрав начальное приближение (x₁⁰, x₂⁰), подставим его в правую часть системы.

Проделав аналогичные операции для (x₁¹, x₂¹), (x₁², x₂²),…, (x₁^k-1, x₂^k-1), получим общую формулу метода простых итераций

2) Сходимость метода Якоби линейная. Более быструю сходимость дает одна из модификаций метода простых итераций – метод Зейделя. Метод Зейделя отличается от метода Якоби тем, что при вычислении k-го приближения к корню используются уже вычисленные на k-ом шаге корни. Применительно к системе двух уравнений формула (3.16) примет вид

Т.е. для вычисления второго корня используются значения первого корня с текущего шага, остальные значения берутся с предыдущего шага.

3) В основе метода Ньютона лежит использование разложений функции F_i(x₁,x₂,..x_i) в ряд Тейлора, причем члены содержащие более высокие порядки производных, отбрасываются.

Рассмотрим реализацию метода Ньютона для системы из двух нелинейных уравнений вида.

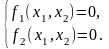
При итерационном нахождении корней каждое последующее значение отличается от предыдущего на некоторую величину . Запишем формально итерационные формулы для двух корней

3.2.Примеры алгебраических уравнений

Алгебраическими уравнениями называют уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные).

Пример: y(x)=x²+3x-10

3.3.Определение трансцендентного уравнения, примеры.

Трансцендентными уравнениями называются уравнения, содержащие тригонометрические, показательные, логарифмические и др.

Пример: y(x)=x²-sin(10x)

3.4.Определение корня уравнения

Корнем уравнения называется число, которое при подстановке в уравнение преобразуется в верное тождество.

3.5.Для чего производится процедура отделения корней нелинейного уравнения и предварительное исследование уравнений. Примеры.

Может быть выполнено графически, либо аналитически. Графический способ предназначен для небольшого количества нелинейных функций f(x), которые могут быть заменены двумя:f(x)=f₁(x)-f₂(x)

f(x)=e^x-x

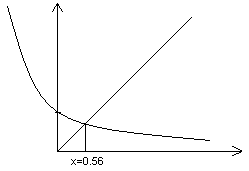
e^-x=x

Б олее общим способом отделения корней является аналитический метод, основанный на теореме интервалов. Если на непрерывной на [a,b] функции f(x) имеет на концах интервала разные знаки, то внутри интервала [a,b] находится, по крайней мере, один корень.

Если при этом на интервале [a,b] существует производная, не меняющая знак f(x)>0 , то внутри [a,b] только один корень.

3.6.Основные понятия итерационного процесса

Итерационный процесс состоит в последовательном уточнении начального приближения x₀. Каждый такой шаг называется итерацией. В результате итераций находиться последовательность приближенных значений корня x₁, x₂, x₃,…,x_n. Если эти значения с ростом n приближаются к истинному значению корня, то говорят, что итерационный процесс сходиться.

Итерационные методы – это методы последовательных приближений.

Алгоритм нахождения корня уравнения с помощью итерационного метода состоит из двух этапов:

1. отыскание приближенного значения корня или содержащего его отрезка;

2. уточнение приближенного значения до некоторой заданной степени точности.

3.7.Сформулируйте теорему о сходимости метода простых итераций

Теорема.

Если норма Якобиана , то итерационный процесс сходится.

Матрица Якоби (якобиан) для системы двух переменных имеет вид

В зависимости от принятой нормы 1 или 2 условия сходимости имеют вид

3.8.Укажите классы нелинейных уравнений.

Существует 2 вида нелинейных уравнений: алгебраические и трансцендентные.

Алгебраическое уравнение- это многочлен или полином, т.е содержит х в какой-либо степени.

Трансцендентное уравнение- содержит специальные функции, типа exp, логарифмич и т.д.

3.9.Приведите примеры алгебраических и трансцендентных уравнений

Алгебраическими уравнениями называют уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные).

Пример: y(x)=2x⁴+6x-10

Трансцендентными уравнениями называются уравнения, содержащие тригонометрические, показательные, логарифмические и др.

Пример: y(x)=x²-sin(10x)/ln(x²)

3.10.Выделите этапы решения нелинейного уравнения.

Алгоритм нахождения корня уравнения с помощью итерационного метода состоит из двух этапов:

1) отыскание приближенного значения корня или содержащего его отрезка (определение приближенного значения по графику);

2) уточнение приближенного значения до некоторой заданной степени точности (по методам Якоби, Зейделя, Ньютона).

3.11.Какие существуют методы отделения корней нелинейного уравнения.

Отделение корней может быть выполнено графически, либо аналитически. Графический способ предназначен для небольшого количества нелинейных функций f(x), которые могут быть заменены двумя f(x)=f₁(x)+f₂(x). Абсциссы точек пересечения графика с осью ОХ будут значениями корней.

Более общим способом отделения корней является аналитический метод, основанный на теореме интервалов: Если непрерывная на [a,b] функция f(x) имеет на концах интервала разные знаки, то внутри интервала [a,b]находится, по крайней мере, один корень

Если при этом на интервале существует производная, не меняющая знак f’(x)>0 либо f’(x)<0, то внутри [a,b] существует только один корень.

3.12.Перечислите интервальные методы нахождения корней.

Метод хорд, метод половинного деления (дихотомии), метод касательных, метод простых итераций.

3.13.Сформулируйте теорему интервалов.

Если непрерывная на [a,b] функция f(x) имеет на концах интервала разные знаки, то внутри интервала [a,b]находится, по крайней мере, один корень

Если при этом на интервале существует производная, не меняющая знак f’(x)>0 либо f’(x)<0, то внутри [a,b] существует только один корень.

3.14.Приведите геометрическую иллюстрацию метода дихотомии

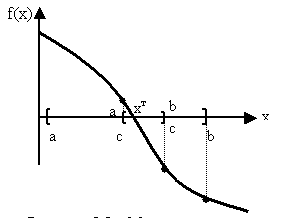
3 .15.Приведите геометрическую иллюстрацию метода хорд

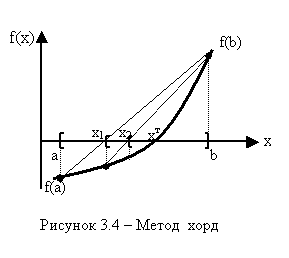
3.16.Приведите геометрическую иллюстрацию метода касательных (Ньютона).

3.17.Приведите геометрическую иллюстрацию метода простых итераций для решения нелинейных уравнений

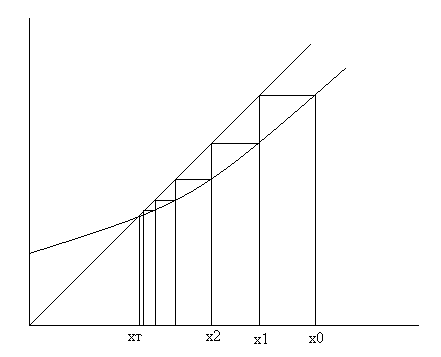
3.18.Дайте понятие итерационного процесса, сходимости и погрешности методов.

Итерационный процесс: итерационный метод, отделение корней, правило останова.

3.19.Приведите достаточные условия метода простых итераций для решения нелинейного уравнения и систем нелинейных уравнений

Достаточным условием сходимости метода простых итераций является условие |φ’(x)|<1 , выполненное для любого х, принадлежащего некоторому отрезку [a,b] , содержащему корень уравнения.