6.5 Регрессионное уравнение

Регрессионное уравнение – аналитическая функция, позволяющая строить функцию при любых значениях аргумента и получение нового набора значений функции, более гладких, чем исходные данные, но только при исходных значениях аргумента. Является одним из средств сглаживания данных.

Регрессионная функция является оптимальной в среднеквадратическом смысле. Графически это с войство соответствует построению линии визуально усредняющей экспериментальные данные.

На рисунке точками () показаны экспериментальные данные, сплошной линией – функция их соединяющая, пунктирной- линия регрессии.

6.6 Метод наименьших квадратов

При эмпирическом (экспериментальном) изучении функциональной зависимости одной величины у от другой х производят ряд измерений величины у при различных значениях величины х. Полученные результаты можно представить в виде таблицы, графика:

X	x1	x2	…	xn
Y	y1	y2	…	yn

Задача заключается в аналитическом представлении искомой функциональной зависимости, то есть в подборе функции, описывающей результаты эксперимента.

Особенность задачи состоит в том, что наличие случайных ошибок измерений делает неразумным подбор такой формулы, которая точно описывала бы все опытные значения, то есть график искомой функции не должен проходить через все экспериментальные точки. Эмпирическую формулу обычно выбирают из формул определенного типа:

Таким образом, задача сводится к определению параметров a, b, c,… формулы, в то время как вид формулы известен заранее из каких-либо теоретических соображений или из соображения простоты аналитического представления эмпирического материала. Пусть выбранная эмпирическая зависимость имеет вид

с явным указанием всех параметров, подлежащих определению. Эти параметры а₀, а₁, а₂,…, а_n нельзя определить точно по эмпирическим значениям функции y₀, y₁, y₂,…, y_k, так как последние содержат случайные ошибки.

Таким образом, речь может идти только о получении достаточно хороших оценок искомых параметров. Метод наименьших квадратов (МНК) позволяет получить несмещенные и состоятельные оценки всех параметров а₀, а₁, а₂,…, а_n.

Суть МНК

Рассмотрим суть метода МНК на примере построения аппроксимирующего (регрессионного) уравнения  (x), включающего 2 базисные функции {1, sinx}:

 (x)=a0+a1 sin(x).

В качестве критерия аппроксимации, т.е. правила, которому удовлетворяет регрессионное уравнение, выбрана среднеквадратическая погрешность :

(1)

где n – число измерений функции y(x), в узлах xi.

Выражение - определяет разницу между исходной (табличной) и результирующей (аппроксимирующей) функциями.

Функция, удовлетворяющая критерию (1) является наилучшей в среднеквадратическом смысле, а метод ее нахождения – МНК. Для выполнения условия (1) необходимо, чтобы при полученных параметрах a0, a1 функция невязок S(a0, a1) имела стационарную точку, т.е.

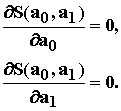
Перепишем критерий (1) с учетом конкретного вида  (x):

.

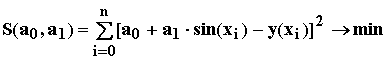Найдем частные производные:

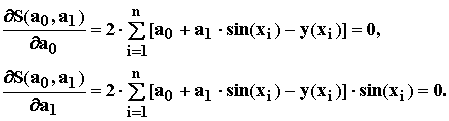
Перепишем праве части последних уравнений, вынося за знак суммы неизвестные коэффициенты регрессионного уравнения а0, а1:

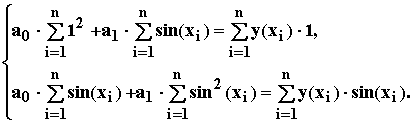
Полученные уравнения представляют собой систему линейных алгебраических уравнений относительно неизвестных а0, а1. Запишем систему в матрично- векторном виде:

.

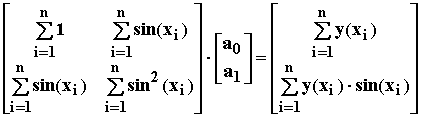Или

где матрица Ф носит название матрицы Грамма и зависит только от базисных функций, вектор определяется измеренными значениями y(xi) и базисными функциями.

Отсюда вектор искомых коэффициентов регрессионного уравнения:

.