6.1 Основные задачи аппроксимации функций

Существует 3 задачи приближения данных:

1. Интерполяция – требуется построить ф-ию, которая проходит как можно ближе к измеренным значениям.

2. Сглаживание данных – получение ф-ии, устраняющей попавшие в измерения шумы и погрешности. Получение более гладкой ф-ии.

3. Экстраполяция – получение значений функции или процесса вне интервалов наблюдения. Прогнозирование возможно как для значений, находящихся перед наблюдаемым интервалом, так и для значений, находящихся после него.

Цель аппроксимации (приближенной замены) заключается в аналитическом представлении искомой функциональной зависимости, то есть в подборе формулы, корректно описывающей экспериментальные данные. Возникает в случае, когда требуется по эмпирическим (экспериментальным) данным построить функциональную зависимость в виде формулы.

6.2 Понятие интерполяции данных, критерий интерполяции

Интерполяция данных: требуется построить функцию, которая как можно ближе проходит через все значения экспериментальных данных. Иногда под интерполяцией понимают получение данных в промежутках между узлами [x_i, x_i+1].

Пусть на отрезке [a, b] заданы (n+1) точка a=x₀<x₁ <…<x_n=b и (n+1) значение функции f(x): {f₀, f₁ , …,f_n}. f_i=f(x_i).

Значения x_i называются сеткой узлов, f_i – решетчатой или таблично заданной функцией.

В задаче интерполяции требуется по табличным значениям (x_i, f_i) построить функцию  (x) такую, что значения  (x) легко вычисляются при x  [a, b] и при этом

 (x_i)=f(x_i), i 1,n.

Последнее равенство носит название критерия интерполяции;

f(x) – интерполируемая функция;

(x) – интерполирующая функция.

Интерполирующая функция (x) может быть получена в двух видах:

• в виде аналитического выражения (формула);

• численно, т.е. в виде отдельных числовых значений для x  [a, b].

при получении аналитической зависимости (x) строится в виде линейной комбинации элементарных (базисных) функций

,

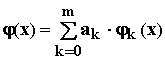где  _k(x) – базисные функции;

a_k – коэффициенты разложения по базисным функциям.

6.3 Сплайн- аппроксимация

Наиболее современным аппаратом интерполяции являются сплайн функции.

Сплайн – многочлен, склеенный из отдельных кусков. На каждом интервале отдельный кусок многочлена, а в узловых точках сетки эти куски сопрягаются или склеиваются. Сплайн значительно увеличивает точность интерполяции.

6.4 Фильтрация и сглаживание данных

Сглаживание данных: получение функции, устраняющей случайные погрешности, попавшие в экспериментальные данные.

Сглаживание данных возможно в двух вариантах: получение аналитической функции (регрессионного уравнения), позволяющей строить функцию при любых значениях аргумента и получение нового набора значений функции, более гладких, чем исходные данные, но только при исходных значениях аргумента.

Регрессионная функция является оптимальной в среднеквадратическом смысле. Графически это с войство соответствует построению линии визуально усредняющей экспериментальные данные.

На рисунке точками показаны экспериментальные данные, сплошной линией – функция их соединяющая, пунктирной – линия регрессии.

Фильтрация данных позволяет сгладить экспериментальные данные; результат фильтрации не содержит погрешностей; данные после фильтрации строятся в виде отдельных числовых значений.