5.20 Методы Рунге для решении задачи Коши (идея и особенности)

Эти методы явл-ся общими методами реш-я задачи Коши. Они полумерны. С их помощью реализованы все спец. функции в матем. пакетах. Объясняется эта популярность простыми вычислительными схемами. Для получения значения в т-ке y(k+1) требуется значение , т.е. в предыдущих точках. Платой за столь малую информативность метода является некоторая их громосткость и обращенность к левой части в дифф-ом ур-ии на каждом шаге. При сложной правой части f(x,y) приходится выполнять большой объем вычислений.

5.21 Метод Эйлера для решения задачи Коши

Метод рядов, не требующий вычисления производных правой части уравнения выглядит так:

Имеем ур-е (*), где x_n+1 = x_n + h.

Чтобы выполнить это условие, производные y⁽ⁱ⁾(x), i = 2, 3,..., m, входящие в правую часть уравнения (*), можно заменить по формулам численного дифференцирования их приближенными выражениями через значение функции y' и учесть, что

y'(x) = f [x, y(x)].

В случае m = 1 приближенное равенство (*) не требует вычисления производных правой части уравнения и позволяет с погрешностью порядка h² находить значение y(x_n+ h) решения этого уравнения по известному его значению y(x_n). Соответствующее одношаговое правило можно записать в виде:

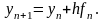Это правило впервые было построено Эйлером и носит его имя. Иногда его называют также правилом ломаных или методом касательных.

5.22 Принцип Рунге для оценки шага при решении задачи Коши

Принцип Рунге. Если приближенный метод имеет порядок погрешности m, то погрешность можно приближенно оценить по формуле:

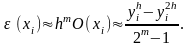
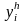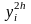В этой формуле O(x_i) – главный член погрешности, и - приближенные решения в точке x_i, найденные с шагом h и 2h соответственно.

Для оценки погрешности численного решения применим принцип Рунге, позволяющий оценить погрешность на каждом шаге по формуле:

где s – порядок метода Рунге-Кутта, y_h, y_2h –значения интегральной кривой, вычисленные с шагом h и 2h. Оценка по этой формуле должна быть проведена для каждой точки k=1,2,…n.

5.23 Источники погрешности методов Рунге - Кутта

6.1	Основные задачи аппроксимации функций 525
6.2	Понятие интерполяции данных, критерий интерполяции
6.3	Сплайн- аппроксимация
6.4	Фильтрация и сглаживание данных
6.5	Регрессионное уравнение
6.6	Метод наименьших квадратов
6.7	Экстраполяция данных
6.8	Показатели эффективности аппроксимации
6.9	Решение задач аппроксимации в пакете MathCad
6.10	Приведите понятие аппроксимации функций
6.11	Приведите понятие интерполирования данных (глобальная и локальная интерполяция)
6.12	Что такое сглаживание данных
6.13	Что такое экстраполяция данных
6.14	Что такое аппроксимация экспериментальных или табличных данных.
6.15	В чем разница между глобальной и локальной интерполяцией.
6.16	Что такое экстраполяция и прогноз данных.
6.17	В чем состоит основная идея сплайн аппроксимации.
6.18	Критерий метода наименьших квадратов
6.19	Укажите основные показатели качества аппроксимации.
6.20	Процедуры интерполирования данных в ППП MathCad
6.21	Понятие регрессионного уравнения
6.22	Что такое базисные функции? Пример базисных функций.
6.23	Суть метода наименьших квадратов
6.24	Понятие аппроксимации
6.25	Показатели эффективности приближения данных