5.7 Решение систем дифференциальных уравнений

Решение дифференциального уравнения n-го порядка сводится к решению системы n дифференциальных уравнений 1-го порядка. Рассмотрим методику этого метода на примере дифференциального уравнения 2-го порядка:

, начальные условия: ; Требуется найти функцию f(x), при x [0, 1].

Введем следующие обозначения:

и продифференцируем левую и правую часть этой системы =>

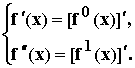
Или с учетом введенных обозначений и исходного дифференциального уравнения:

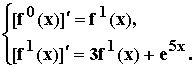, при начальных условиях:

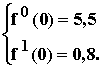
Итак, получили систему двух дифференциальных уравнений 2-го порядка. Для примера приведем фрагмент решения этой системы в пакете Mathcad:

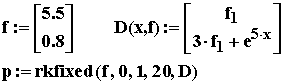
5.8 Дайте определение задачи Коши

Задача Коши для уравнения состоит в нахождении частного решения ур-я, удовлетворяющего заданным начальным условиям. Другое определение: обыкновенные дифф-е ур-я имеют множ-во решений, чтобы найти единственное, необходимы дополнительные усл-я. Если доп. усл-е задано в одной т-ке, то оно наз-ся Задачей Коши.

5.9 Дайте определение краевой задачи

Задача наз-ся краевой если для нахождения частного решения дифф-го ур-я задано несколько начальных(граничных) условий.

5.10 Приведите классификацию дифференциальных уравнений

Основные виды дифф-х ур-ий: допускающие разделение переменных, с разделяющимися переменными, однородные, линейные первого порядка, Бернулли, в полных дифференциалах.

С разделенными переменными:

1.простейшие ДУ I порядка y’=f(x)

=>dy=f(x)dx=> => , y₀=y(x₀)(можно найти частное решение.)

2.. Дифференциальное уравнение вида f(x)dx+φ(y)dy=0, где f(x), φ(y)-непрерывные функции то уравнение называется, уравнение с разделенными переменными

Уравнение с разделяющимися переменными:

ДУ вида M₁(x)*M₁(y)dx+ M₂(x)*M₂(y)dy=0, где М₁(х), М₁(у), М₂(х), М₂(у) – непрерывные функции это уравнение называется разделяющимися переменными (зависят отдельно только от х или у).

Однородное уравнение:

Однородное уравнение первого порядка, где f(x, y)-однородная функция степени 0(ноль).

Опр-е: ДУ первого порядка Р(х, у)dx+Q(x, y)dy=0(1) или уравнение если оно разрешается относительно называется однородным.

Линейные:

Опр-е: Линейным ДУ 1-го порядка называется уравнение линейное относительно неиз-ой функции и ее производной.

В общем случае оно может быть записано в виде:

где Р(х), f(x)-заданные непрерывные функции.

Уравнение Бернулли:

y'+P(x)y=f(x)yⁿ, n≠0.1 (3)

t(x)=y^1-n (сводит к линейному уравнению)

t'=(1-n)y^-n y' преобразуем уравнение (3)

ДУ в полных дифференциалах:

ДУ вида M(x,y)dx+N(x,y)dy=0(4) называется уравнением полных дифференциалов.

5.11 В чем разница между аналитическим и численным решением дифференциального уравнения?

Аналитическое решение- основано на интегрировании дифф-го ур-я => интегрируемая прямая есть сама ф-я. Однако этим способом можно решить очень ограниченный круг задач.

При численном решении интегрируемую кривую y(x) находим лишь в отд. значениях в узловых точках аргумента x.

5.12 Сформулируйте постановку задачи Коши

Пусть задано обыкн. ур-е 1-го порядка, т.е. , , .

Эта задача может быть решена двумя способами: 1) аналитически; 2) численно(приближенно).

5.13 В чем состоит основная идея методов Рунге- Кутта

В этом методе интервал [a,b] разбивается на n частей. Приближенное значение функции y(x_k) возможно найти лишь в этих внутренних точках интервала, т.е. на сетке узлов x_k:

a=x₀<x₁<x₂<…<x_i<…<x_n=b.

5.14 Определите локальную и глобальную погрешность задачи Коши

5.15 Запишите формулы Рунге- Кутта 1 и 2-го порядков

I порядок (метод Эйлера):

- формула Эйлера позволяет, начиная с начальных условий {x0, y0} получить последовательность приближений к решению дифференциального уравнения { y1, y2, …,y n}.

II порядок:

Возможны 2 варианта формул Рунге- Кутта II порядка:

а) б)

Вариант а(метод Эйлера-Коши) формулы является аналогом формулы трапеции (численное интегрирование), вариант б(модифицированный метод Эйлера) – средних прямоугольников.

5.16 Запишите формулы Рунге- Кутта 1 и 4-го порядков

I порядок (метод Эйлера):

- формула Эйлера позволяет, начиная с начальных условий {x0, y0} получить последовательность приближений к решению дифференциального уравнения { y1, y2, …,y n}.

IV порядок:

Аналог – формулы Симпсона.

5.17 В чем состоит идея метода Рунге- Кутта с адаптивным шагом

Если известно, что искомая функции быстро меняется, то целесообразно использовать метод Рунге - Кутта с переменным (адаптивным) шагом. При этом переменный шаг используется только при нахождении функции y(x).

5.18 В чем состоит идея решения дифференциального уравнения высокого порядка

Решением дифф-го ур-я n-го порядка наз-ся любая n раз дифференцируемая функция y=y(x), которая при подстановке в уравнение, обращает его в тождество.

5.19 Какие известны процедуры решения задачи Коши в ППП MathCad ау

В пакете Mathcad существует несколько процедур решения задачи Коши. Основные из них следующие:

rkfixed(yO,tO,ti,M,D) - метод Рунге-Кутта с фиксированным шагом;

rkadapt(yO,to,ti,M,D) - метод Рунге-Кутта с переменным шагом;

buistoer(yO,to,ti,M,D) - метод Булирша-Штера;

уO - вектор начальных значений в точке to размера NxI; tO - начальная точка расчета; ti - конечная точка расчета; M - число шагов, на которых численный метод находит решение; D - векторная функция размера NxI двух аргументов - скалярного t и векторного у. При этом у - искомая векторная функция аргумента t того же размера NxI. Каждая из приведенных функций выдает решение в виде матрицы размера (M+i)x(N+i). В ее левом столбце находятся значения аргумента t, делящие интервал на равномерные шаги, а в остальных N столбцах - значения искомых функций уO(t), y!(t),..., y_N-i(t), рассчитанные для этих значений аргумента. Поскольку всего точек (помимо начальной) M, то строк в матрице решения будет всего M+1.