1.1	Что такое погрешности числа и вычислений
1.2	Дайте определение погрешности
1.3	Приведите определение абсолютной и относительной погрешности
1.4	Укажите формы записи абсолютной погрешности
1.5	Приведите определение значащих цифр числа
1.6	Укажите форму записи числа с фиксированной запятой
1.7	Укажите форму записи числа с плавающей запятой
1.8	Напишите определение верных и сомнительных цифр числа
1.9	Понятие точного и приближенного числа
1.10	Привести примеры устранимой и неустранимой погрешности.
1.11	Указать основные источники погрешностей.
1.12	Привести формы записи абсолютной погрешности.
1.13	Как вычислить относительную погрешность, зная абсолютную?
1.14	Привести формы записи числа с фиксированной и плавающей запятой. Привести примеры записи.
1.15	Что такое сомнительные и верные цифры числа. Способы их вычисления.
1.16	Что такое значащие цифры числа.
1.17	Сформулировать основную задачу теории погрешностей.
1.18	Дать понятие разрядной сетки ЭВМ.
1.19	Погрешность математической модели
1.20	Погрешность вычислительного метода
1.21	Источники погрешности численного результата
1.22	Погрешность округления ЭВМ
1.23	Погрешность сложной функции
1.24	Понятие вычислительного эксперимента
1.25	Погрешность дискретизации
1.26	Оценить абсолютную погрешность функции F=x2 - y-3
1.27	Сколько значащих цифр в числе 1223,0034
1.28	Как влияет влияет способ представления чисел в ЭВМ на точность расчетов

1.1 Что такое погрешности числа и вычислений.

Погрешности числа и вычислений ето устранимые и неустранимые погрешности.

Неустранимые погрешности – погрешность математической модели и погрешности исходгых данных, т.е. погрешность числа.

Устранимые погрешности – погрешности вычислительных методов и ЭВМ,т.е. погрешности вычислений.

1.2. Дайте определение погрешности.

Погрешности – незначительные отклонения результата от истинного значения.

1.3. Приведите определение абсолютной и относительной погрешности.

Относительной погрешностью приближенного числа Х* называют величину , определяемую выражением

.

Абсолютной погрешностью приближенного числа Х* называют величину , которая является ограничением разности

.

Т.е. Х*-  Х   Х*+ .

Другая форма записи абсолютной погрешности Х=Х* .

1.4. Укажите формы записи абсолютной погрешности.

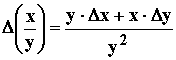
1.5. Приведите определение значащих цифр числа.

Значащими цифрами числа Х* называют все цифры в его записи, начиная с первой ненулевой слева.

Любое число можно представить в виде:

Х*=  ₁   ⁿ +  ₂   ^{n -1} + ... +  _m   ^n-m+1,

где ₁ –  первая значащая цифра;

– основание системы счисления (2, 8, 10, 16);

        0  _i .

 

Пример. 2,718 = 2  10⁰ + 7  10^-1 + 1  10^-2 + 8  10^-3.  = 10;   ₁=2;   ₂=7;   ₃=1;   ₄=8;   n=0.

 

1.6. Укажите форму записи числа с фиксированной запятой.

Фиксированая запятая позволяет получить большую точность, чем с плавающей при одинаковой разрядной сетке

∆= *^n-k+1 =[0,5;1]

1.7. Укажите форму записи числа с плавающей запятой.

x*=M^p М-мантиса

р-степень(положительная, отрицательная, ноль)

n – показатель при первой значащей цифре

1.8. Напишите определение верных и сомнительных цифр числа.

Значащая цифра _к считается верной, если выполняется неравенство

     ^n-к+1 ,       0    1,

в противном случае _к – сомнительная цифра.

1.9. Понятие точного и приближенного числа.

Число Х называется точным значением числа.

Приближенным числом Х* называется число, незначительно отличается от точного Х и заменяющее последнее в вычислениях.

1.10. Привести примеры устранимой и неустранимой погрешности.

Неустранимые погрешности – погрешность математической модели и погрешности исходгых данных.

Устранимые погрешности – погрешности вычислительных методов и ЭВМ.

1.11. Указать основные источники погрешностей.

а) Связанные с самой постановкой математической задачи.

б) Связаные с наличием бесконечных процессов в математичеком анализе.

в) Связанные с наличием в математических формулах числовых параметров, значения которых могут быть определены лишь приближенно.

г) Связаные с системой счисления.

д) Связанные с действиями над приближенными числами.

1.12. Привести формы записи абсолютной погрешности.

1.13. Как вычислить относительную погрешность, зная абсолютную.

.

То есть относительную погршеность разделить на приближенное значение числа.

1.14. Привести формы записи числа с фиксированной и плавающей запятой. Привести примеры записи.

Число с фиксированной запятой.

∆= *^n-k+1 =[0,5;1]

Число с плавающей запятой.

x*=M^p М-мантиса

1/ ≤М<1 р-степень(положительная, отрицательная, ноль)

n – показатель при первой значащей цифре