7.2. Расчёт реакций опор и изгибающих моментов тихоходного вала

На вал действуют силы в вертикальной плоскости:

F_r – радиальная сила на шестерне (колесе); F_a – осевая сила на шестерне (колесе); F_м – сила от муфты;

В горизонтальной плоскости:

F_t – окружная сила на шестерне (колесе).

Принимаем Н

Исходные данные:

d = 0,108м, l₁ = 0,032 м, l₂ = 0,032 м, l₃ = 0,078 м,

Fr = 269,28 Н, F_a = 96,57 Н, F_t =740 Н, F_м = 800 Н

7.2.1. Реакции опор в вертикальной плоскости

Сумма моментов в точке А равняется 0:

МАу = 0 Frl₁ + Fa0,5d + RВy(l₁ +l₂) – F_м(l₁ +l₂ +l₃) = 0;

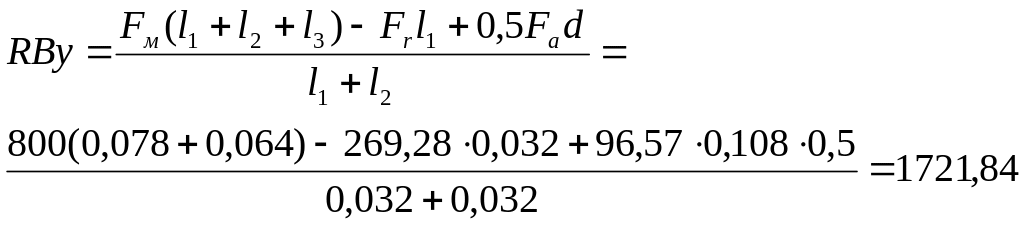
Сумма моментов в точке В равняется 0:

МВу = 0, - Frl₂ + Fa0,5d + RАy(l₁ +l₂) – F_мl₃ = 0;

Проверка: У = 0, -RAy + F_r + RBy – F_м = 0;

- 1191,12 + 269,28 + 1721,84 – 800 = 0

Строим эпюру изгибающих моментов в вертикальной плоскости:

Му_2слева = - RAyl₁ = - 1191,12 · 0,032 = - 38,11 Нм

Му_{2справа} = - F_м(l₂+l₃) + RByl₂ = -800(0,032+0,078)+1721,84· 0,032 =

- 43,09 Нм

Му₃ = - F_мl₃ = - 800 · 0,078 = - 62,4 Нм

7.2.2. Реакции опор в горизонтальной плоскости

Сумма моментов в точке А равняется 0:

МАх = 0, - Ftl₁ + RBx(l₁ + l₂) = 0;

Н

Сумма моментов в точке В равняется 0:

МВх = 0, F_tl₂ - RAx(l₁ + l₂) = 0;

Н

Проверка: X = 0, RAx - F_t +RBx = 0;

370 – 740 + 370 = 0

Строим эпюру изгибающих моментов в горизонтальной плоскости:

Мх₂ = - RAхl₁ = - 370 · 0,032 = - 11,84 Нм

7.2.3. Суммарные реакции опор в подшипниках:

Н

Н

7.2.4. Опасное сечение находится под колесом

Концентратор напряжений – шпоночный паз

Суммарный изгибающий момент в опасном сечении

М_и = Нм.

Эпюры изгибающих и крутящего моментов тихоходного вала

8. Проверочный расчёт валов на прочность

Для каждого из установленных предположительно опасных сечений определяем расчётный коэффициент запаса прочности S и сравниваем его с допускаемым [S]=1,3…2,1 [1]:

Где: s и s - коэффициенты запаса прочности соответственно по нормальным и касательным напряжениям

; ,

где: (_-1)_D, (_-1)_D – пределы выносливости вала в рассматриваемом сечении;

_a, _a – амплитуды напряжений цикла;

_m, _m – средние напряжения цикла;

_, _ - коэффициенты чувствительности к асимметрии цикла напряжений.

Пределы выносливости вала в рассматриваемом сечении

; ,

где: _-1,, _-1 – пределы выносливости материала вала для гладких образцов при симметричном цикле изгиба и кручения;

(K_)_D ,(K_)_D – коэффициенты концентрации напряжений для данного сечения вала.

Коэффициенты (K_)_D и (K_)_D вычисляются по формулам:

; ,

где: К_, К_ - эффективные коэффициенты концентрации напряжений;

K_d – коэффициент влияния абсолютных размеров поперечного сечения вала;

K_F - коэффициент влияния шероховатости;

K_v – коэффициент влияния поверхностного упрочнения.

При симметричном цикле напряжений изгиба и отнулевом цикле касательных напряжений

, _m = 0; , _m=0

где: Wн и Wк – осевой и полярный моменты сопротивления сечения вала.

При учёте осевой силы (например, на червяке), вызывающей растяжение вала

_m=F_a/A, где А – площадь опасного сечения вала.

8.1. Проверочный расчёт валов на прочность

8.1.1. . Проверочный расчёт быстроходного вала

Выбираем материал вала – сталь 20Х, термообработка – закалка ТВЧ

_-1 = 410 МПа, _-1 = 240 МПа, табл. 10.2 [1]

К_ = 1,7 для вала-шестерни, табл. 10.9 [1];

К_ = 1,55 для вала-шестерни, табл. 10.9 [1];

K_d = 0,8 при диаметре вала d = 50 мм, табл. 10.3 [1];

K_F =1,15 при Ra = 0,8…3,2 мкм, табл. 10.3 [1];

K_v = 1,7 при данной термообработке, табл. 10.5 [1].

Коэффициенты концентрации напряжений для данного сечения вала

Пределы выносливости вала в рассматриваемом сечении

(МПа) (МПа)

Осевой момент сопротивления сечения вала

(мм³)