§3. Игры с матрицами, отличающимися порядком строк и столбцов

Пусть две игры определены матрицами

,

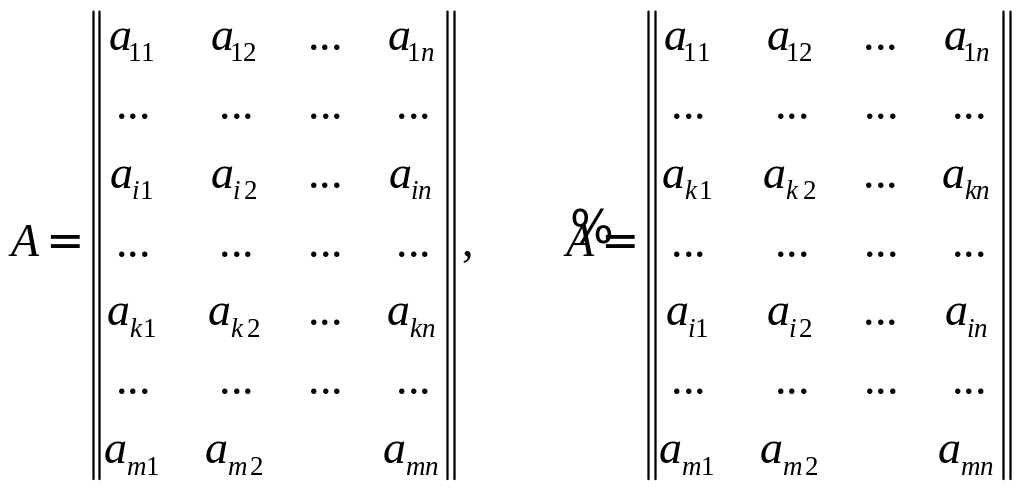где матрица получена из перестановкой в строк с номерами и .

Теорема 3.1. Пусть – решение и – цена игры с матрицей .

Тогда пара , где получено перестановкой в векторе координат с номерами и , , является решением игры с матрицей , а ее цена совпадает с .

Доказательство. Построим квадратную размерности матрицу , которая получена из единичной матрицы в результате перестановки строк с номерами и . Заметим, что матрица невырожденная, т.к. ее определитель равен –1, и что

, , , , . (3.1)

,

Обозначим -мерный вектор, все координаты которого равны единице через . Тогда неравенства (2.31), которые выполняются по условиям теоремы, запишем для удобства вычислений в векторно-матричном виде

. (3.2)

Выберем , . В соответствии с этим и с условиями (3.1), (3.2)

. (3.3)

Кроме того, . Второе из неравенств (3.2) показывает, что все координаты вектора не превышают . Умножение вектора слева на переставляет его координаты с номерами и . Значит, все координаты вектора не больше . Значит, . Поскольку это неравенство и неравенство (3.3) выполняются для одного и того же числа , то согласно следствию теоремы 2.2.1 об оптимальных смешанных стратегиях число является ценой, а – решением игры с матрицей . Теорема доказана.

Аналогично доказывается

Теорема 3.2. Пусть – решение и – цена игры с матрицей ,а матрица получена перестановкой в матрице столбцов с номерами . Тогда пара , где , а получено перестановкой в векторе координат с номерами , будут решением игры с матрицей , а цена этой игры совпадает с .

Теоремы 3.1 и 3.2 позволяют, естественно, установить связь между решениями игр с матрицами, различающимися порядком любого количества строк и столбцов.

Игры, матрицы которых отличаются лишь порядком строк и столбцов называются изоморфными.

§4. Простые стратегии

В данном параграфе изучим свойства таких смешанных стратегий, которые играют существенную роль в отыскании крайних точек множества оптимальных стратегий, и, следовательно, в отыскании всех решений матричной игры.

Определение 4.1. Если для игры Г, определенной матрицей , и числа существует такая смешанная стратегия , что

, , (4.1)

то стратегию будем называть простой, соответствующей числу , и говорить, что игра Г допускает простую стратегию, соответствующую этому числу.

Если простая смешанная стратегия соответствует цене игры, то в силу теоремы 2.2.1 оптимальна для первого игрока.

Аналогичным является

Определение 4.2. Если для игры Г, определенной матрицей , и числа существует такая смешанная стратегия , что

, , (4.2)

то стратегию будем называть простой, соответствующей числу , и говорить, что игра Г допускает простую стратегию, соответствующую этому числу.

Если простая смешанная стратегия соответствует цене игры, то в силу теоремы 2.2.1 стратегия оптимальна для второго игрока.

В силу следствия теоремы 2.2.1 обратное утверждение справедливо в следующем виде. Если игра допускает простые стратегии , соответствующие одному и тому же числу , то – цена игры, – ее решение.

Определение 4.3. Если – простые оптимальные стратегии в матричной игре , то пара называется простым решением этой игры. В этом случае говорят, что игра допускает простое решение.

Изучим особо случай, когда платежная матрица является квадратной и невырожденной. В этом случае .

Теорема 4.1. Пусть – квадратная невырожденная матрица размерности и – сумма всех элементов матрицы , , – решения систем (4.1), (4.2), соответственно. Тогда

, .

Доказательство. Каждая из систем (4.1), (4.2) имеет единственное решение

, . (4.3)

Умножая равенства (4.3) скалярно на вектор , получим

, . (4.4)

Легко заметить, что

, , .

Отсюда и из равенств (4.4) следует утверждение теоремы.

Заметим, что теорема справедлива для любой квадратной невырожденной матрицы, т.к. при доказательстве ее не использовались игровые понятия.

Обсудим те выводы, которые можно сделать из доказанной теоремы для теории игр.

Во-первых, решения (4.3) систем (4.1), (4.2) могут быть смешанными стратегиями в игре, определенной матрицей только при и .

Во-вторых, если при решение системы (4.1) или системы (4.2) имеет неотрицательные координаты, то оно является в силу теоремы 4.1 смешанной стратегией в игре, определенной матрицей .

В-третьих, если обе системы (4.1), (4.2) имеют неотрицательные решения при , то в силу теоремы 4.1 и условий оптимальности (теорема 2.2.1) они являются оптимальными стратегиями, а - ценой игры с матрицей .

Заметим, что решения (4.3) систем (4.1), (4.2) могут иметь отрицательные координаты и тогда они не являются смешанными стратегиями.

Пример 4.1. Пусть игра определена матрицей

.

Тогда

и . Тогда при согласно теореме 4.1 сумма координат решения системы (4.2) будет равняться единице. Система (4.2) имеет вид

ее решение . Хотя сумма координат этого решения равна единице, но оно не может быть смешанной стратегией, хотя бы потому, что имеет отрицательную координату.

Пример 4.2. Пусть игра определена матрицей

.

Игра с такой матрицей имеет седловую точку (1,2) и цену . Поэтому ее решение в смешанных стратегиях можно записать в виде , , в чем легко убедиться, проверив выполнение условий теоремы 2.2.1 оптимальности. Однако игра не допускает простых смешанных стратегий, т.к. и . Поэтому в силу теоремы 4.1 системы (4.1), (4.2) не имеют решений, сумма координат которых равна единице. Заметим, что оптимальные стратегии , не являются простыми.

Пример 4.3. Пусть игра определена матрицей

.

Игра имеет седловую точку (1,2) и, следовательно, цену . Как и в предыдущем примере, ее решение в смешанных стратегиях можно записать в виде , . Убедимся, что эта игра имеет и простые смешанные стратегии. Действительно, системы (4.1), (4.2) при имеют, соответственно, вид

.

Их решения являются простыми смешанными оптимальными стратегиями.

Определение 4.3. Оптимальная стратегия , называется вполне смешанной, если для всех ( ).

Из определений 4.2 и 4.3 и теоремы 2.2.2 о дополняющей нежесткости вытекает следующее

Утверждение. Если в игре с матрицей и ценой оптимальная стратегия является вполне смешанной, то для оптимальной стратегии выполняются равенства

,

т.е. оптимальная стратегия второго игрока является простой.

Аналогичное утверждение справедливо и для оптимальной стратегии второго игрока.