1.4. Некоторые виды степенного среднего

Среднее арифметическое входит в группу средних величин, объединенных названием - степенное среднее. В эту группу, наряду со средним арифметическим, входят среднее гармоническое, среднее геометрическое, среднее квадратичное и т. д.

Среднее гармоническое

Среднее гармоническое чисел x₁, x₂, ..., x_n - число, обратная величина которого является средним арифметическим обратных величин данных чисел, т. е. число

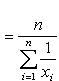или .

Среднее гармоническое необходимо в том случае, когда наблюдения, для которых мы хотим получить среднее арифметическое, заданы обратными значениями.

Среднее геометрическое

Среднее геометрическое положительных чисел x₁, x₂, ..., x_n - число, равное арифметическому корню n-й степени из их произведения, т. е.

или .

Среднее геометрическое используют тогда, когда среднее значение вычисляют для значений, заданных через некоторые равные промежутки времени (рост или снижение успеваемости, заработной платы, вклада в банке за несколько лет). Среднее геометрическое применяют тогда, когда переменная с течением времени изменяется примерно с одинаковым соотношением между измерениями. Среднее геометрическое применяют также тогда, когда отдельные значения в статистической совокупности удалены от других значений; это меньше влияет на среднее геометрическое по сравнению со средним арифметическим, а потому дает более правильное представление о среднем.

1.5. Ограничения при работе с мерами центральной тенденции

1. Следует всегда помнить, что меры центральной тенденции отражают адекватно реальную ситуацию, только если мы имеем дело с однородной совокупностью:

• для выборок, имеющих более чем одну моду, любая мера центральной тенденции, включая среднее, будет недостаточно хороша. Центральной тенденции в таком распределении просто не существует;

• две одинаковые меры центральной тенденции можно сравнивать, только если они имеют относительно одинаковые распределения. Нельзя сказать, что средние в рядах 20, 20, 20 и 2, 18, 40 равны;

• нельзя с уверенностью сказать, что среднее показывает нам «типичный» случай, если не знать кривой распределения.

2. Моду незачем вычислять, когда частоты всех наблюдаемых значений почти равны.

3. Выбирая меру центральной тенденции, нужно руководствоваться знанием ее свойств, общей формой распределения и, наконец, здравым смыслом. Например, если речь идет о выборке из большой совокупности, где интересующая исследователя переменная-признак распределена нормально, наилучшим показателем будет среднее. Если в унимодальном распределении встречаются крайние значения, могущие значительно повлиять на среднее, нужно отдать предпочтение медиане.

Среднее арифметическое является хорошей мерой центральной тенденции для количественных данных, не имеющих выбросов; медиана - для порядковых данных и для количественных данных, в том числе и при наличии выбросов. Для номинальных данных подобной характеристикой является мода. Она применяется как для неупорядоченных категорий, так и для упорядоченных, и для количественных данных.

Выбор меры центральной тенденции в зависимости от типа измерительной шкалы

Тип шкалы	Меры центральной тенденции

В одном из учебников приведен анекдот, который обобщает множество проблем, возникающих в процессе применения разных мер центральной тенденции.

Однажды пятеро мужчин сидели рядом на скамейке парка. Двое были бродягами, имущество которых выражалось в 25 центах. Третий был рабочим, чей счет в банке и другое имущество составляли 2000 долларов. Четвертый владел 15 000 долларов в различных формах. Пятый же был мультимиллионером с чистым доходом 5 000 000 долларов. Поэтому модальный актив группы составил 25 центов. Эта цифра точно характеризует двоих, но является чрезвычайно некорректной для трех других. Медиана, составляющая 2 000 долларов, несколько меняет дело для всех, кроме рабочего. Среднее, 1 003 400,10 долларов, не является вполне удовлетворительным даже для мультимиллионера. Если мы должны выбрать одну меру центральной тенденции, возможно, это была бы мода, которая точно описывает 40 процентов группы. Однако если сказать, что «модальный актив пяти лиц, сидящих на скамье парка, равен 25 центам», то нам пришлось бы сделать вывод о том, что общий актив группы приблизительно составляет 1,25 доллара, что меньше фактического более чем на пять миллионов долларов. Очевидно, нет меры, адекватной этим «странным соседям по скамейке», которые просто не имеют «центральной тенденции».

Другой вывод из анализа противоречий этого анекдота состоит в том, что для группы с пятью значениями не требуется никакая обобщающая статистика.