
- •1.1.Числові розв’язки системи лінійних алгебраїчних рівнянь. Правило Крамера.
- •2.1..Мінор матриці. Алгебраїчне доповнення до елеметна . Вираз для визначення матриці через його доповнення.
- •2.2. Диференціальне рівняння для коливних процесів в акустині, електродинаміці та для встановлених процесів (на прикладі поля електричного поля).
- •5.1.Складання математичної таблиці для значень функції . Реалізація методу складання математичної таблиці для значень функції в середовищі Mathcad, Matlab, Maple, Exel.
- •6.1.Метод січних (хорд) розв’язку (знаходження коренів) нелінійних рівнянь. Метод простих ітерацій. Приклад.
- •6.2..Метод сіток для рівнянь диференціального рівняння в частинних похідних параболічного типу (на прикладі рівняння теплопровідності).
- •2.Поняття про числові методи математичної статистики.
- •9.1.Метод половинного ділення в задачі уточнення кореня нелінійного рівняння. Абсолютна похибка методу.
- •9.2.Початкові та граничні умови для рівнянь в частинних похідних (на прикладі рівняння теплопровідності).
- •8.1.Формула ейлера та її розв’язок з розкладами в ряди функцій sinx та cjsx.
- •8.2.Використання в задачах диференціювання інтерполяційних многочленів.
- •1.Визначник (детермінант) матриці, алгоритм його обчислення.
- •11.2.Побудова диференціального рівняння для математичного маятника та для маятника поперечних коливань.
- •12.1.Предмет «Чисельні методи», його роль в сучасній науці.
- •13.2.Сплайн-інтерполяції. Поліноміальний сплайн.
- •14.1.РядМаклорена для функцій sinx та cosx.
- •15.1.Основні задачі числових методів алгебри.
- •16.1.Постановка задачі та етапи числових методів розв’язку нелінійних рівнянь (знаходження коренів нелінійних рівнянь).
- •16.2.Різницевий метод розв’язку крайової задачі для лінійного звичайного диференціального рівняння другого порядку.
- •17.1.Метод Гауса розв’язків системи лінійних алгебраїчних рівнянь. Реалізація методів знаходження розв’язків системи лінійних алгебраїчних рівнянь в середовищі Mathcad, Matlab, Maple, Exel.
- •18.1.РядМаклорена для функції однієї змінної. Приклад розкладу в ряд для функції .
- •19.1.Знаходження коренів функції багатьох змінних: градієнтний метод.
- •19.2.Метод сіток для рівнянь диференціального рівняння в частинних похідних еліптичного типу (на прикладі рівняння двох змінних).
- •20.1.Способи відділення коренів нелінійних рівнянь.
- •21.1.Реалізація методів лінійної алгебри в середовищі Mathcad, Matlab, Maple, Exel.
- •23.1.Реалізація методів знаходження коренів функцій однієї і багатьох змінних в середовищі Mathcad, Matlab, Maple, Exel.
- •22.1.Метод Ньютона розв’язку (знаходження коренів) нелінійних рівнянь. Спрощений метод Ньютона.
- •22.2.Наближені методи розв’язку крайових задач: метод коллокацій, метод найменших квадратів.
- •26.1.Чисельний метод знаходження числа пі.
- •26.2.Поліномний кубічний сплайн. Похибка наближення поліноміальними сплайнами.
- •24.1.Ряд Тейлора для функції однієї змінної на основі її ряду Тейлора. Приклад.
- •24.2.Постановка задачі чисельного інтегрування функцій. Квадратурні формули прямокутників, трапецій, Симсона. Похибки чисельного інтегрування.
- •1 1.Числові розв’язки системи лінійних алгебраїчних рівнянь. Правило Крамера.
- •2.Класифікація диференціальних рівнянь в частинних похідних.
- •2 1.Мінор матриці. Алгебраїчне доповнення до елеметна . Вираз для визначення матриці через його доповнення.
24.1.Ряд Тейлора для функції однієї змінної на основі її ряду Тейлора. Приклад.
Пусть функция f(x) имеет на отрезке [a,b] непрерывные производные до n-1 - го порядка, а в интервале (a,b) - существует n - ая производная функции f (x), тогда для любых x0 и x из [a,b] существует такая точка ξ, лежащая между точками х0 и х, что
|
|
|
||||
|
Выражение |
|
|
|
|
|
называется многочленом Тейлора степени n-1 для функции f(x) в окрестности точки x0.
Выражение Rn(ξ,x) называют остаточным членом формулы Тейлора.
24.2.Постановка задачі чисельного інтегрування функцій. Квадратурні формули прямокутників, трапецій, Симсона. Похибки чисельного інтегрування.
Дамо
означення інтегралу. Нехай на відрізку
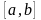 задана функція
задана функція
 .
За допомогою точок
.
За допомогою точок
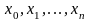 розіб’ємо відрізок
на п
елементарних
відрізків
розіб’ємо відрізок
на п
елементарних
відрізків
 (
( ),
причому
),
причому
 .
На кожному з цих відрізків виберемо
довільну точку
.
На кожному з цих відрізків виберемо
довільну точку
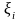 (
( )
та знайдемо добуток
)
та знайдемо добуток
 значення функції в цій точці
значення функції в цій точці
 на довжину елементарного відрізка
на довжину елементарного відрізка
 :
:
 .
(1) Складемо
суму всіх таких добутків:
.
(1) Складемо
суму всіх таких добутків:
 .
(2)
.
(2)
Сума
 називається інтегральною сумою.
Означеним інтегралом від функції
називається інтегральною сумою.
Означеним інтегралом від функції
 на відрізку
називається границя інтегральної суми
при необмеженому збільшенні кількості
точок розбиття; при цьому довжина
найбільшого з елементарних відрізків
прямує до нуля:
на відрізку
називається границя інтегральної суми
при необмеженому збільшенні кількості
точок розбиття; при цьому довжина
найбільшого з елементарних відрізків
прямує до нуля:
 .
(3)
.
(3)
В
багатьох випадках, коли підінтегральна
функція задана в аналітичному вигляді,
означений інтеграл вдається визначити
безпосередньо за допомогою невизначеного
інтеграла (вірніше, первісної) за
формулою Ньютона-Лейбніца. Вона полягає
в тому, що означений інтеграл дорівнює
приросту первісної
 на відрізку інтегрування:
на відрізку інтегрування: .
.
Але на практиці цією формулою часто не можна скористатися внаслідок основних причин: Аналітичний вигляд функції не дозволяє безпосередньо провести інтегрування згідно (4), оскільки первісну неможливо виразити через елементарні функції.
Значення
функції
задані лише на фіксованій скінченій
множині точок
 ,
тобто функція задана у вигляді таблиці
і є дискретною.
,
тобто функція задана у вигляді таблиці
і є дискретною.
У цих випадках використовують методи чисельного інтегрування. Вони основані на інтерполяції підінтегральної функції деяким більш простішим виразом, наприклад многочленами.
Метод прямокутників
Найпростішим
методом чисельного інтегрування є
метод прямокутників. В ньому здійснюється
заміна означеного інтеграла інтегральною
сумою. За точки
можуть вибиратися ліві (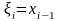 )
або праві (
)
або праві ( )
границі елементарних відрізків.
Позначивши
)
границі елементарних відрізків.
Позначивши
 ,
,
 ,
отримаємо наступні формули метода
прямокутників відповідно до цих двох
випадків:
,
отримаємо наступні формули метода
прямокутників відповідно до цих двох
випадків:
 ,
(5)
,
(5)
 .
(6)
.
(6)
Широко поширеним та найбільш точним є вигляд формули прямокутників, що використовує значення функції в середніх точках елементарних відрізків (метод середніх прямокутників):
 ,
(7)
,
(7)

Метод
трапецій Метод
трапецій використовує лінійну
інтерполяцію, тобто графік функції
подається у вигляді ламаної, що з’єднує
точки
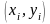 .
В цьому випадку площа всієї фігури
(криволінійної трапеції) складається
з площ елементарних прямолінійних
трапецій. Площа кожної такої трапеції
рівна:
.
В цьому випадку площа всієї фігури
(криволінійної трапеції) складається
з площ елементарних прямолінійних
трапецій. Площа кожної такої трапеції
рівна: .
Додаючи всі ці рівності, отримуємо
формулу трапецій для чисельного
інтегрування:
.
Додаючи всі ці рівності, отримуємо
формулу трапецій для чисельного
інтегрування:
 .
(8)
Важливим частинним випадком розглянутих
формул є їх застосування при чисельному
інтегруванні з постійним кроком
.
(8)
Важливим частинним випадком розглянутих
формул є їх застосування при чисельному
інтегруванні з постійним кроком
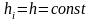 (
).
Формули прямокутників і трапецій в
цьому випадку приймають відповідно
вигляд
(
).
Формули прямокутників і трапецій в
цьому випадку приймають відповідно
вигляд
 (9)
(9)
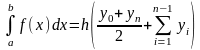 (10)
(10)
Метод парабол (метод Сімпсона)
Розіб’ємо
відрізок інтегрування
на парне число рівних частин з кроком
 .
На кожному відрізку
.
На кожному відрізку
 ,
,
 ,
... ,
,
... ,
 ,
... ,
,
... ,
 підінтегральну
функцію
замінимо інтерполяційним многочленом
другого степеня:
підінтегральну
функцію
замінимо інтерполяційним многочленом
другого степеня:
 .
.
Коефіцієнти
цих квадратних тричленів можуть бути
знайдені з умов рівності многочлена в
точках
відповідним табличним даним
 .
За
.
За
 можна прийняти інтерполяційний многочлен
Лагранжа другого степеня, що проходить
через точки
можна прийняти інтерполяційний многочлен
Лагранжа другого степеня, що проходить
через точки
 ,
,
,
,
 :
:
 .
.
Елементарна
площа
може бути знайдена за допомогою
означеного інтеграла. Враховуючи
рівність
![]() ,
отримаємо
,
отримаємо

 .
.
Провівши такі розрахунки для кожного елементарного відрізку , просумуємо отримані вирази:
 .
.
Дані
вирази для
 приймається за значення означеного
інтегралу:
приймається за значення означеного
інтегралу:
 .
(11)
.
(11)
Отримане співвідношення називається формулою Сімпсона.


