Доказательство основной теоремы

Теперь нетрудно завершить доказательство основной теоремы.

Пусть ƒ(x, y, z) - симметрический многочлен и аx^ky^lz^m - одно из его слагаемых. В силу симметричности многочлена ƒ(x, y, z), он содержит вместе с этим слагаемым и всю орбиту 0(x^ky^lz^m), взятую с коэффициентом а. Таким образом,

ƒ(x, y, z)=а·0(x^ky^lz^m)+ƒ₁(x, y, z),

где ƒ₁(x, y, z)- некоторый многочлен, который, симметричен и содержит меньше членов, чем ƒ(x, y, z). Из ƒ₁(x, y, z) можно также выделить орбиту одного из его членов и так далее После конечного числа шагов мы разложим многочлен ƒ(x, y, z) на сумму орбит отдельных одночленов.

Итак,

Любой симметрический многочлен ƒ(x, y, z) есть сумма конечного числа орбит одночленов.

А так как каждая орбита выражается через , , , то и любой симметрический многочлен может быть выражен через , , . Тем самым основная теорема полностью доказана.

Все доказательство является конструктивным: оно содержит сравнительно несложный алгоритм, позволяющий любой симметрический многочлен выразить через , , .

Найдем выражение симметрического многочлена

ƒ(x, y, z)=x³+y³+z³-4xyz+2x²y+2xy²+2x²z+2xz²+2y²z+2yz²

через , , . Мы имеем:

ƒ(x, y, z)=0(x³)-4·0(xyz)+2·0(x²y)=

=( )-4 +2( )=

Обратные степенные суммы

Степенные суммы, соответствующие отрицательным показателем, то есть выражения

s_-k=x^-k+y^-k+z^-k=

(где k=1, 2, 3,…), иногда называют обратными степенными суммами. Их легко выразить через , , , если заметить, что

.( )

Однако можно поступить и по-другому. Достаточно заметить, что формула (1) справедлива для любых значений k (в том числе и отрицательных), поскольку при выводе этой формулы ни каких предположений относительно k не было сделано. Заменяя в формуле (1) k на l+3, легко находим:

( )

С помощью полученной формулы ( ) можно последовательно находить значения обратных степенных сумм:

и так далее Наоборот, имея вычисленные таким образом значения обратных степенных сумм, можно легко находить орбиты 0(x^ky^k), пользуясь формулой ( ):

(x²y²)=

0(x³y³)=

(x⁴y⁴)=

и так далее.

Основные формулы необходимые для решения задач:

x²y+xy²+x²z+xz²+y²z+yz²=

x²y²+x²z²+y²z²=

x³y+xy³+x³z+xz³+y³z+yz³=

Справедливость формул можно проверить, подставив значения , , .

симметрический многочлен уравнение переменное

Применения к элементарной алгебре Решение систем уравнений с тремя неизвестными

Результаты выше сказанного позволяют решать некоторые системы алгебраических уравнений с тремя неизвестными. Если левые части уравнений симметрично зависят от неизвестных x, y,z, то удобно принять , , , за новые неизвестные. Выгода такой замены неизвестных заключается в том, что степени уравнений после замены уменьшаются (поскольку - многочлен второй степени, а - многочлен третьей степени). Иными словами, решение системы относительно новых неизвестных , , проще, чем решение первоначальной системы.

После того как найдены значения величин , , , нужно найти значения первоначальных неизвестных x, y, z. Это может быть сделано с помощью следующей теоремы.

Пусть , , - три произвольных числа. Кубическое уравнение

( )

и система уравнений

( )

связаны друг с другом следующим образом: если u₁, u₂, u₃-корни кубического уравнения, ( ), то система уравнений ( ) имеет шесть решений

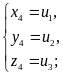
(получающихся друг от друга перестановками) и других решений не имеет; обратно, если x=a, y=b, z=c - решение системы ( ), то числа a, b, c являются корнями кубического уравнения ( ).

Для доказательства этой теоремы нам понадобится следующая лемма.

Если u₁, u₂, u₃ - корни кубического уравнения u³+pu²+qu+r=0, то имеют место соотношения:

u₁+u₂+u₃=-p,₁u₂+u₁u₃+u₂u₃=q, u₁u₂u₃=-r.

Эти соотношения называются формулами Виета для кубического уравнения. Покажем, откуда эти формулы вытекают. Итак, пусть u₁, u₂, u₃ - корни кубического уравнения u³+pu²+qu+r=0; числа u₁, u₂, u₃ могут быть действительными или комплексными. Тогда многочлен u³+pu²+qu+r следующим образом разлагается на множители:

u³+pu²+qu+r=(u-u₁)(u-u₂)(u-u₃).( )

Раскрывая скобки в правой части, находим:

u³+pu²+qu+r=u³-(u₁+u₂+u₃)u²+(u₁u₂+u₁u₃+u₂u₃)u-u₁u₂u₃.

Написанное равенство означает, что слева и справа стоит один и тот же многочлен, то есть что соответствующие коэффициенты в левой и правой частях совпадают. Иными словами,

-(u₁+u₂+u₃)=p,₁u₂+u₁u₃+u₂u₃=q,

-u₁u₂u₃=r,

что и доказывает лемму.

Доказательство теоремы. Если u₁, u₂, u₃ - корни кубического уравнения ( ), то, согласно лемме, имеют место соотношения

u₁+u₂+u₃= ,₁u₂+u₁u₃+u₂u₃= ,₁u₂u₃= .

Но это и означает, что числа x=u₁, y=u₂, z=u₃ составляют решение системы ( ). Еще пять решений получаются из этого перестановками значений неизвестных. То, что других решений система ( ) не имеет, вытекает из последнего утверждения теоремы, которое мы сейчас докажем.

Итак, пусть x=a, y=b, z=c - решение системы ( ), то есть

a+b+c= ,+ac+bc= ,= .

Тогда мы имеем:

Это означает, что числа a, b, c являются корнями кубического уравнения ( ). Теорема доказана.

Замечание. Доказанная теорема показывает также, что если уже найденные значения величин , , , то для нахождения значений первоначальных неизвестных x, y, z (то есть для решения системы ( )) достаточно составить кубическое уравнение ( ) и найти его корни. В учебниках высшей алгебры можно найти формулы для решения кубических уравнений. Однако формулы эти сложны и на практике редко применяются. Чаще всего пытаются найти один корень кубического уравнения, после чего пользуются теоремой Безу:

Остаток от деления многочлена

ƒ(x)=a₀xⁿ+a₁x^n-1+…+a_n

на x-a равен значению этого многочлена при x=a, то есть равен числу

ƒ(a)=a₀aⁿ+a₁a^n-1+…+a_n.

Чтобы доказать эту теорему, разделим многочлен ƒ(x) на x-a. Мы получим частное, которое обозначим через q(x), и некоторый остаток r(x). Этот остаток является многочленом, степень которого меньше степени делителя x-a, то есть равна нулю. Поэтому r(x)=r является числом. Итак,

ƒ(x)=(x-a)q(x)+r.

Чтобы найти число r, положим в этом равенстве x=a. Мы получим ƒ(a)=r. Теорема Безу доказана.

Подчеркнем еще раз, что, решив кубическое уравнение ( ), мы находим сразу шесть решений для первоначальных неизвестных x, y, z: так как в систему ( ) неизвестные x, y, z входят симметрично, то можно переставлять их и в решении.

Рассмотрим пример.

1. Решить систему уравнений

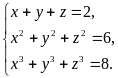
Введем новые неизвестные , , , положив

x+y+z= ,

xy+xz+yz= ,

xyz= .

В силу формул, приведенных в таблице 1, мы имеем для новых неизвестных систему уравнений:

Из этой системы находим:

В развернутом виде эта система записывается так:

x+y+z=2,

xy+xz+yz=-1,

xyz=-2.

Для решения этой системы составляем (согласно теореме) кубическое уравнение

u³-(u₁+u₂+u₃)u²+(u₁u₂+u₁u₃+u₂u₃)u-u₁u₂u₃=0,³-2u²-u+2=0.

Левая часть уравнения раскладывается на множители:

u³-2u²-u+2=(u-2)(u²-1).

Следовательно, корнями этого уравнения являются числа

u₁=2, u₂=1, u₃=-1.

Поэтому наша исходная система имеет шесть решений, получающихся перестановками из решения

x=2, y=1, z=-1.

Заметим, что в некоторых случаях несложная предварительная замена переменных позволяет свести несимметричную систему к симметричной.