12 Система лінійних Алгебраїчних рівнянь, точні і наближені методи їх розв'язку

Система лінійних алгебраїчних рівнянь (СЛАР) — в лінійній алгебрі система лінійних рівнянь виду:

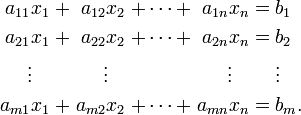
Це система m лінійних рівнянь з n невідомими, де

 є невідомими,

 є коефіцієнтами системи,

 - вільними членами^[1].

Системи лінійних алгебраїчних рівнянь відіграють важливу роль у математиці, оскільки до них зводиться велика кількість задачлінійної алгебри, теорії диференціальних рівнянь, математичної фізики тощо, та областей фізики й техніки, де застосовуються ці математичні теорії.

Множина розв'язків

Розв’язком системи лінійних алгебраїчних рівнянь є будь-яка сукупність дійсних чисел  , яка при підстановці кожне рівняння системи перетворює його втотожність.

Якщо система має хоча б один розв’язок, то вона називається сумісною, і несумісною, якщо не має жодного. Відповідь на питання сумісності системи дає теорема Кронекера-Капеллі.

Сумісна система називається визначеною, якщо вона має єдиний розв’язок, і невизначеною, якщо вона має безліч розв’язків. В останньому випадку кожен її розв’язок називають частковим розв’язком системи. Сукупність усіх часткових розв’язків називають загальним розв’язком системи.

Якщо всі вільні члени  , система лінійних алгебраїчних рівнянь називається однорідною. Однорідна система має очевидний розв'язок, у якому всі  . Цей розв'язок заведено називати тривіальним. Відмінні від тривіального розв'язки існують тільки тоді, коли матриця   вироджена.

Методи роз'язку

Методи розв’язування систем лінійних албераїчних рівнянь можна досить чітко поділити на три групи: точні, ітераційні та ймовірнісні. За Бахваловим (1987 рік), точні методи застосовні до систем з числом змінних до порядку 10⁴, ітераційні — 10⁷.

Точні Методи

До точних методів належать методи, що дають точний результат у припущенні ідеальної арифметики (див. IEEE754). Точні методи можна застосовувати й тоді, коли коефіцієнти й вільні члени рівняння задані в аналітичній, символьній формі.

• Метод послідовного виключення. Найпростішим, хоча важким для практичних застосувань, методом розв'язування системи лінійних алгебраїчних рівнянь є метод послідовного виключення невідомих. Суть його в тому, що із першого рівняння змінна 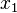  виражається через інші змінні, й підставляється в усі інші рівняння. Це можна зробити, якщо коефіцієнт 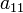  відмінний від нуля. У випадку, якщо він нульовий, можна вибрати інше рівняння, оскільки перестановка рівнянь у системі дає еквівалентну систему. В результаті утворюється нова система рівнянь, в якій рівнянь на одне менше. З цією системою рівнянь можна поступити так само, отримуючи ще меншу систему рівнянь. Продовжуючи так, отримують одне лінійне рівняння, з якого можна визначити одну із змінних, а інші, виключені, виразити через неї.

• Метод Гауса — метод, найчастіше застосовуваний при ручному розв’язуванні СЛАР.

  • Метод Гауса-Жордана - модифікація методу Гауса.

• Метод Крамера (за формулами Крамера) — чисто теоретичний метод, непридатний до практичного використання через обчислювальну складність і малу точність, оскільки вимагає обчислення визначників, а тільки в одному визначнику   доданків. Метод Крамера може застосовуватися для матриць 2×2, або, щонайбільше, 3×3.

• Матричний метод (за допомогою оберненої матриці) - певна теоретична абстракція всіх інших точних методів.

• Метод квадратного кореня — квадратичний метод, який вимагає симетричної матриці системи.

• Метод прогонки зручний для розв’язування систем з тридіагональною матрицею, які часто виникають в задачах математичної фізики.

Ітераційні методи

Ітераційні методи встановлюють процедуру уточнення певного початкового наближення до розв'язку. При виконанні умов збіжності вони дозволяють досягти будь-якої точності просто повторенням ітерацій. Перевага цих методів у тому, що часто вони дозволяють досягти розв'язку з наперед заданою точністю швидше, а також розв'язувати більші системи рівнянь. Суть цих методі полягає в тому, щоб знайти нерухому точку матричного рівняння:

,

еквівалентного початковій системі лінійних алгебраїчних рівнянь. При ітерації   в правій частині рівняння заміняється, наприклад, у методі Якобі (метод простої ітерації) на наближення, знайдене на попередньому кроці:

.

Збіжність ітераційної процедури досягається вибором матриці  , що залежить від задачі. Умови збіжності конкретні для кожного конктретного метода.

Серед ітераційних методів можна відзначити найпопулярніші:

• Метод Якобі (метод простої ітерації);

• Метод Зейделя (інколи називають метод Гауса-Зейделя);

• Метод релаксації;

• Багатосітковий метод;

• Метод Монтанте;

• Метод Абрамова (використовується для розв'язування невеликих систем);

• Метод узагальнення мінімальних лишків;

• Метод біспряжених градієнтів;

• Стабілізований метод біспряжених градієнтів;

• Квадратичний метод спряжених градієнтів;

• Метод квазі-мінімальних лишків.