2.5 Обозначение посадок на чертежах, посадки предпочтительного применения

Глава 3. Расчет и назначение посадок для гладких цилиндрических соединений

3.1 Посадки с натягом

Посадки с натягом предназначены для получения неподвижных соединений под нагрузкой. Они образуются как в системе отверстий (СА), так и в системе вала (СВ), сочетанием полей допуска основных деталей и не основных с основными отклонениями от p до z. Неподвижность соединения обеспечивается предварительным (до сборки) натягом (N):

(3.1)

где

расчетный диаметр гладкого вала;

– расчетный диаметр гладкого отверстия.

Соотношение этих диаметров должно обеспечить такой натяг, чтобы под воздействием силы Z или момента М или комбинированной нагрузки M и Z соединение осталось неподвижным.

Изобразим изготовленный гладкий цилиндрический вал с диаметром , на сборку с этим валом поступает отверстие, которое имеет несколько меньший диаметр . Причем для наглядности изобразим радиальное изображение натяга, т.е. на сборке вал и отверстие имеют одну ось (рис. 3.1).

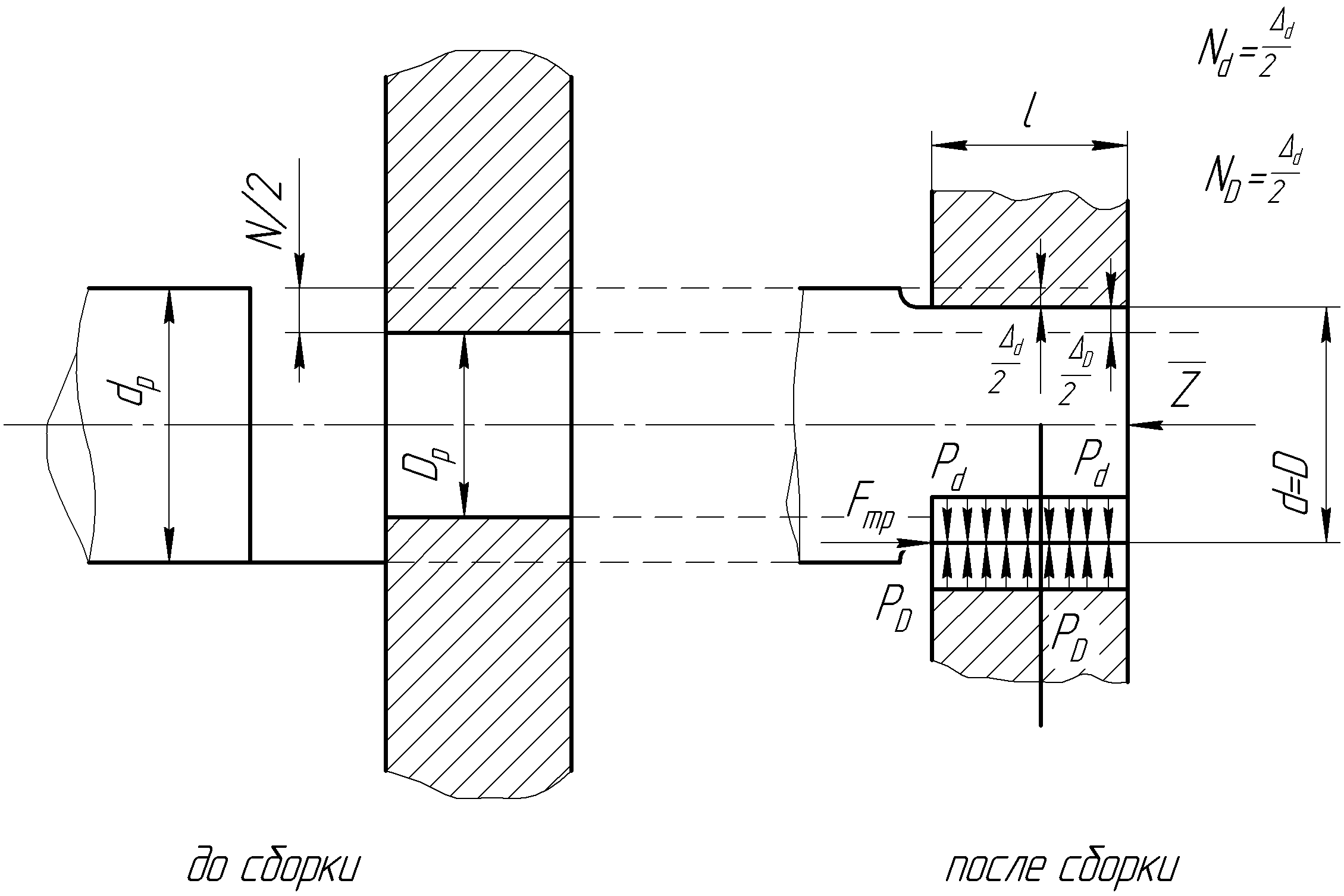
Рисунок 3.1 – Контактные давления при посадке с натягом

Нетрудно видеть, что поскольку натяг есть разница расчетных диаметров вала и отверстия, то у нас в данном случае половина натяга и внизу половина натяга, а в целом он образует натяг как разницу между соответствующими диаметрами,

Представим себе, что было осуществлена операция сборки. В соединение под действием отверстия вал, очевидно, будет сжиматься.

Вал либо механически напрессовывается на отверстие или отверстие напрессовывается на вал, либо с помощью тепловых эффектов – вал и отверстие охлаждаются, вследствие чего вал сжимается, а отверстие расширяется. Затем они соединяются, деталь помещается в нормальную температуру, выравнивается, и происходит деформация вала на сжатие, отверстия на расширение. И, наконец, образуется соединение, общий диаметр которого не принадлежит ни к диаметру отверстия, ни к диаметру вала.

Пунктиром на рисунке показаны исходные диаметры отверстия и вала. Изобразим деформации, которым были подвергнуты обе детали (рис. 3.1).

Таким образом, вал сжался на величину:

Отверстие расширилось на величину:

В результате в соединении образовался общий диаметр d = D, диаметр соединения. Видно, что сумма деформаций представляет собой натяг:

(3.2)

Обозначим длину контакта через l, тогда площадь контакта S равна:

(3.3)

В результате сборки детали образуются два поля давления: со стороны отверстия на вал и со стороны вала на отверстие, которые будут условно равномерными, т. к. не мы не будем рассматривать концевые эффекты.

Рассмотрим случай, когда отверстие будет действовать на вал. Величину давления обозначим через . В противоположную сторону будет действовать . В результате давления появляется сила нормальной реакции опоры. Подействуем на вал некоторой внешней нагрузкой Z, в результате в соединении возникнет противодействующая ей сила трения .

Таким образом, на соединение после сборки действуют следующие силы.

На вал – внешняя сила Z и со стороны отверстия действует сила трения F_тр, причем сила трения возникает за счет контактного давления, которое связано с натягом.

, (3.4)

Совершенно очевидно, что чем больше натяг, а он, как известно, является регулируемым параметром, тем больше контактное давление и выше сила нормальной реакции опоры, значит больше сила трения, следовательно, соединение может сопротивляться большей внешней нагрузке.

Свяжем перечисленные параметры аналитическими выражениями.

Пусть необходимо рассчитать для заданной нагрузки величину натяга , которая обеспечивает неподвижное соединение под этой нагрузкой.

Посадки с натягом в основном работают в упругой области, в которой выполняется закон Гука: напряжение в образце пропорционально его линейной деформации.

, (3.5)

где

Е – модуль упругости первого рода или модуль Юнга;

– напряжение;

– относительная деформация.

Данный закон справедлив для одномерного случая.

Французский ученый Ламэ получил решение для цилиндрических тел:

, (3.6)

где

- коэффициент Ламэ или модуль упругости второго рода,

Данное выражение записано для вала.

Аналогично для отверстия:

. (3.7)

В последнем выражении в знаменателе использовали d, т. к. в соединении диаметр вала d равен диаметру отверстия D.

Выразим из уравнений (3.6) и (3.7) абсолютные деформации вала и отверстия. Используя условие равенства давлений (3.4), запишем:

(3.4а)

Получили связь абсолютных деформаций с величиной контактного давления, величину которого необходимо определить.

Используя выражение (3.2), получим:

. (3.8)

Таким образом, получили решение, которое связывает искомую величину давления с натягом.

Определим силу трения.

Под действием давления Р возникает сила трения , равная произведению коэффициента трения на силу реакции опоры, которая, в свою очередь, равна произведению контактного давления на площадь контакта.

; (3.9)

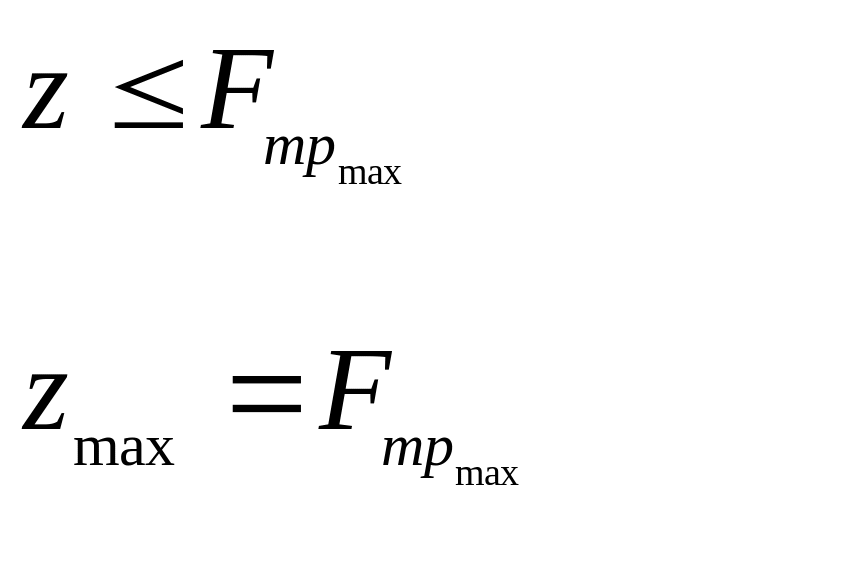(3.10)

Очевидно, что при превышении внешней силой максимальной силы трения, в соединении возникнет подвижность (кризис). До наступления кризиса всегда сила трения будет равна внешней силе.

Условие неподвижности соединения заключается в не превышении активной силой максимально возможной силы трения .

Используя полученные выше выражения, рассмотрим алгоритм расчета минимального расчетного натяга.

Из выражения (3.10) определяем предельную силу трения, затем из уравнения (3.9) – необходимую для этого величину контактного давления Р. Из формулы (3.6) – минимальный расчетный натяг, который обеспечивает выполнение (3.10). Это прямая задача. Существует и обратная, в которой от натяга определяют величину силы трения.

Для обеспечения неподвижности соединения необходимо, чтобы натяг, возникающий в нем, превышал минимальный.

У натяга существует не только нижняя, но и верхняя граница, наличие которой обусловлено разрушением материала.

Условия разрушения, может быть сформулировано, следующим образом: максимальное давление (аналог напряжений) в соединении, при котором еще не наступает разрушение, должно быть меньше предела текучести или иного предела, который ограничивает прочность деталей:

, (3.11)

где А - некоторый коэффициент; - предел текучести.

Тогда, зная из условия (3.8) найдем .

.

При превышении этого натяга может возникнуть разрушение либо вала, либо отверстия.

В реальных условиях необходимо ввести поправки на шероховатость деталей, на температурные деформации (деталь собрана при нормальных условиях, а может эксплуатироваться в других), действие центробежных сил и.т.п.

Например, соединение собрано в неподвижном варианте, на стенде, а затем деталь (турбина) вращается, возникают центробежные силы, которые приводит либо к уменьшению, либо к увеличению натяга, или же соединение было собрано в нормальных условиях, а эксплуатироваться будет, например, при температуре .

Например, поправка на шероховатость опирается на понятие функциональных размеров - - размеры шероховатых деталей, которые в соединении будут функционировать также как и гладкие (рис. 3.2).

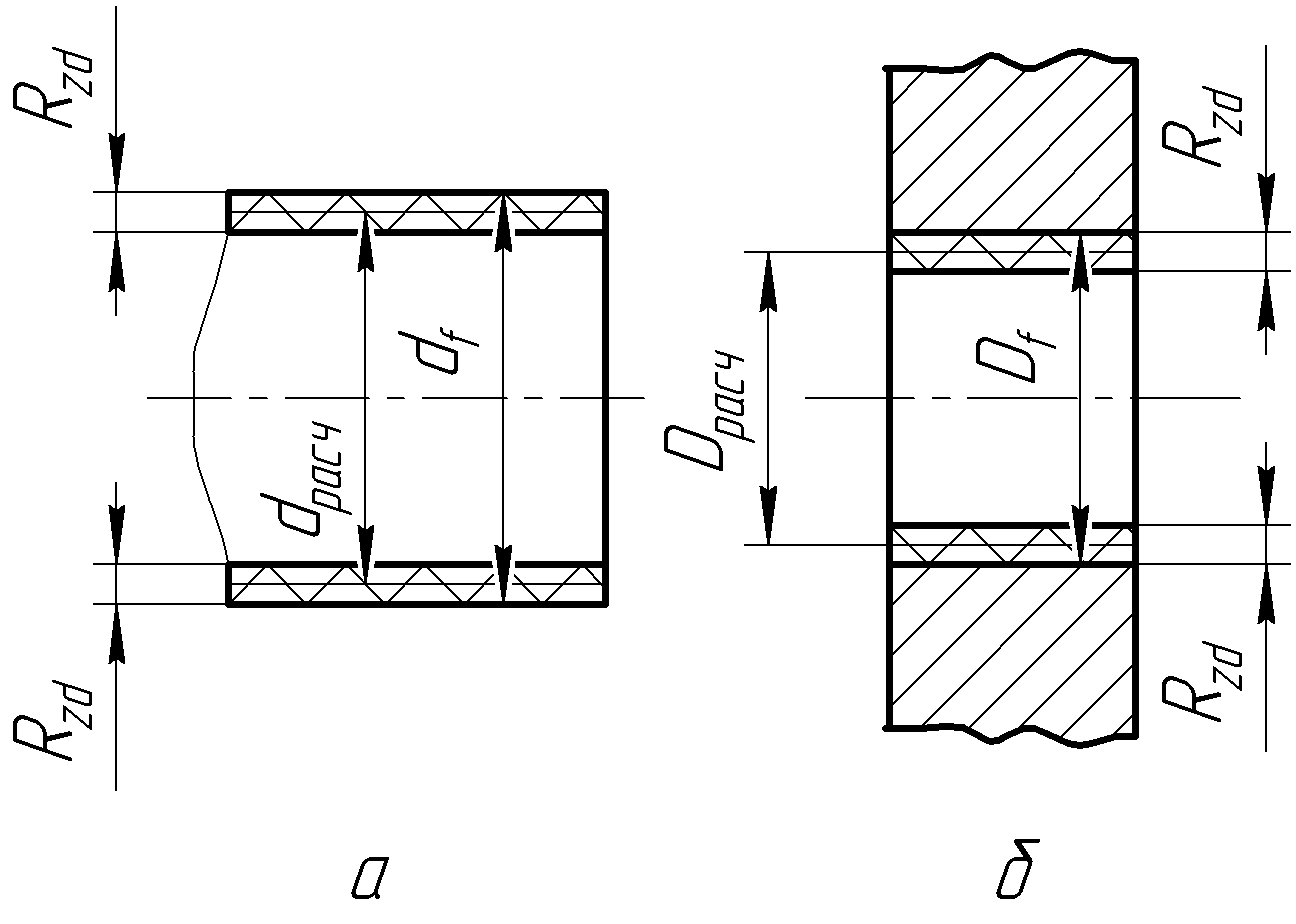
Рисунок 3.2 – Поправки на шероховатость при натяге:

на валу (а) и в отверстии (б)

Тогда

(3.12)

где - коэффициент, учитывающий отличие к сопротивлению сжатия гладкого и шероховатого валов (снятие неровностей).

Аналогично для отверстия.

(3.13)

Таким образом

(3.14)

Для деталей изготовленных из одного материала можно принять

.

Тогда условие выбора посадок с натягом можно сформировать следующим образом:

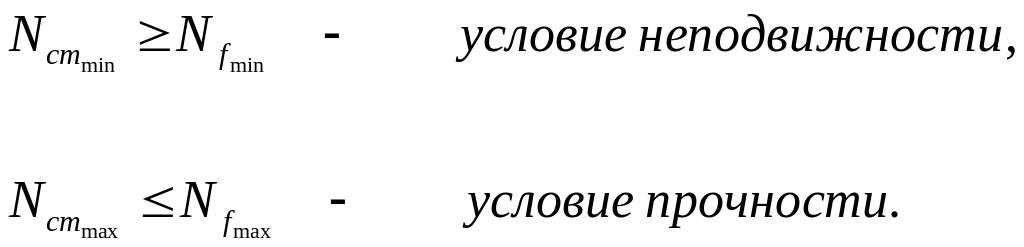
Примеры применения посадок с натягом.

1. Легкие прессовые посадки.

- в СА.

- в СВ.

Такие посадки обеспечивают небольшие натяги и используются для соединения тонкостенных деталей, когда допускаются либо небольшие смещения, либо используются дополнительное крепление (шпонки, шлицы).

2. Средне прессовые посадки

– в СА.

Аналогично в системе вала.

Эти посадки могут воспринимать значительные статические нагрузки.

3. Тяжелые прессовые посадки

- в СА.

Посадки воспринимают значительные реверсивные и ударные нагрузки.