1.4 Погрешность и точность изготовления деталей. Степень точности (квалитет детали, единица допуска)
Под погрешностью изготовления понимается разность между действительным размером детали и наилучшим, т.е. обеспечивающим оптимальное функционирование изделия. Обычно наилучший размер расположен в середине поля допуска:
(1.9)
Точность - степень приближения действительного размера детали к оптимальному.
Пусть изготовлена партия из n
деталей по одному и тому же чертежу.
В силу случайных погрешностей размеры
деталей в партии отличаются друг от
друга. Если причины появления погрешностей
носят случайный характер, например
отклонение температуры окружающей
среды, неоднородность физико-механических
свойств материала заготовки, разброс
в режимах обработки в связи с неточностью
их воспроизведения станком, то такие
погрешности называются случайными.
Пусть каждая из этих деталей имеет
некоторый диаметр Di
(
),
отягощенный случайной погрешностью. В
большинстве случаев распределение
изготовленных деталей, например по D,
отвечает закону нормального распределения
погрешностей или закону Гаусса:
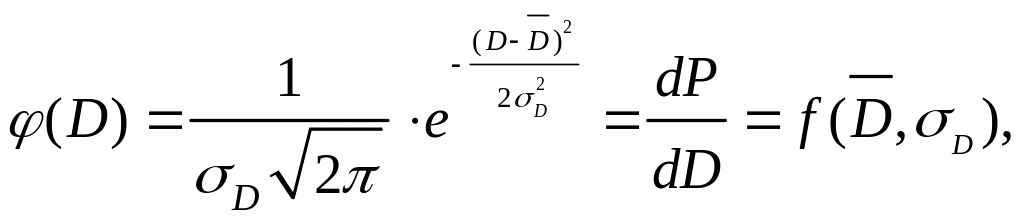(1.10)
где
-
плотность вероятности;
-
математическое ожидание,
;
- среднее квадратичное отклонение,
;
-
дисперсия, параметр, характеризующий
величину случайных погрешностей.
Анализируя формулу (1.10), можно убедиться,
что плотность вероятности достигает
максимума при
:
;
(1.11)
(1.12)
Где
- функция Лапласа;
- квантиль Гаусса; (
)
- доверительный интервал.
Приведем некоторые распространенные значения функции Лапласа:
;
Рисунок 1.6 – Распределение действительных размеров партии деталей с диаметром В по закону Гаусса
Площадь под кривой (вероятность появления значения измеренной величины) в интервале от -∞ до +∞ всегда равна единице (рис. 1.6).
В технологии обычно выбирают такое
оборудование, чтобы вероятность появления
действительного размера детали внутри
интервала
составляла 0,997. В этом случае:
=
,
(1.13)
где
- доверительный интервал.
Для большинства производств выполняется это правило- правило 6σ.
Выясним, что следует понимать под понятием «точность». Когда мы обозначаем величину допуска, то она является абсолютной величиной, возникает вопрос о приемлемости допуска, для ответа на который необходимо знать номинальный размер детали и ее назначение.
Величина допуска определяется по формуле:
(1.14)
где i – единица допуска, зависящая от номинального размера детали.
Зависимость единицы допуска от номинального размера определяется эмпирической формулой, полученной на основании многочисленных исследований:
,
(1.15)
где D измеряется в мм, а i - в мкм.
По оси ординат откладывается единица допуска (i), а по оси абсцисс номинальный размер детали (D) (рис. 1.7).
Зависимость допуска от номинального размера носит непрерывный и монотонный характер. Следует подчеркнуть, что речь здесь идет не о допуске в целом, а только о единице допуска. Данная зависимость показывает, что если изделие изготавливается на одном и том же оборудовании, с одинаковыми режимами обработки и режущими инструментами, то с увеличением диаметра точность этого изделия падает, т.е. единица допуска возрастает.
В ГОСТах непрерывный ряд номинальных размеров разделен на интервалы, внутри которых единица допуска сохраняет постоянное значение. Границы интервала определяются из условия, что осредненное значение единицы допуска внутри интервала отличается от соответствующих граничных значений не более чем на 5-8%.
Рисунок 1.7 – Зависимость единицы допуска от номинального размера детали
Рассмотрим интервал
и
возьмем на этом интервале среднее
значение
:
.
(1.16)
Присваиваем всему интервалу постоянное
значение единицы допуска i,
которое является функцией среднего
значения диаметра
,
т.е.
.
Величина допуска помимо единицы допуска зависит еще и от квалитета, т.е. от степени точности. Поэтому если изобразить аналогичный график самой величины допуска, то можно наблюдать серию непрерывных и монотонных кривых (рис. 1.8).
Рисунок 1.8 – Зависимость величины допуска от квалитета
Из графика видно, что увеличению допуска Т соответствует рост номинального диаметра D и квалитета q.
Коэффициент «а» является функцией от «q», определяется квалитетом (q) .
.
Установленные 20 квалитетов определяют с одной стороны область проектирования, а с другой - финишную операцию обработки детали, чем больше величина квалитета, тем больше коэффициент а, и, следовательно, грубее изготовлена деталь.
Квалитеты до 4-ого используются в точном машиностроении, изготовлении эталонов высшей пробы и прецизионных станков.
С 5-ого по 8-ой - в авиационной и космической технике.
9-ый - в тепловозах, сельскохозяйственной технике.
С 10-ого по 12-ый - в соединении, где допустимы большие зазоры.
С 13-ого по 18-ый - для свободных размеров.
Например, для 5-ого квалитета соответствующего финишной операции - притирка, доводка, тонкое шлифование, коэффициент а = 7. Для 17-го квалитета, где финишная операция - грубое обтачивание, литье, автоматическая газовая резка, коэффициент а = 1600.