5. Алгоритмы поиска циклов в графе
5.1. Понятие о фундаментальных циклах
Задача построения фундаментального множества циклов тесно связана с нахождением стягивающего дерева. Теперь добавим к стягивающему дереву V, Т графа G = V, E произвольную хорду eЕ \ Т. Тогда отметим, что возникший при этом суграф V, Т {e} содержит в точности один цикл. Будем обозначать этот цикл через Ce. Очевидно, что Ce содержит ребро е. Множество P = {Ce | е Е \ Т} будем называть фундаментальным множеством циклов графа G относительно стягивающего дерева V, Т . Название “фундаментальный” связано с тем фактом, что, каждый цикл графа G можно некоторым естественным способом получить из циклов множества P.
Опишем теперь простой алгоритм нахождения множества фундаментальных циклов. Этот алгоритм основывается на поиске в глубину и имеет структуру, аналогичную рекурсивному алгоритму нахождения стягивающего дерева (алгоритм 4.1).
Каждая новая вершина, встречающаяся в процессе поиска, помещается в стек, представленный таблицей СТЕК, и удаляется из стека после использования. Очевидно, что стек всегда содержит последовательность вершин от рассматриваемой в данный момент вершины v до корня. Для построения дерева выбирается еще не посещенная смежная с v вершина. А уже посещенная и смежная с v вершина u дает нам хорду. Но она находится уже в стеке и, по определению, замыкает цикл. Тогда цикл, замыкаемый ребром {v, u}, представлен верхней группой элементов стека, начиная с v и кончая вершиной u. В этом и заключается идея поиска всех фундаментальных циклов, реализованная в следующем алгоритме.
Алгоритм 5.1. Нахождение множества элементарных циклов графа.
Исходные данные: Граф G=V, Е, представленный соответствиями [v], v V.
Результаты: Множество фундаментальных циклов графа G
procedure ЦИКЛ (v);
(*нахождение фундаментального множества циклов для компонент связности, содержащей вершину v; переменные d, num, СТЕК, , wgn – глобальные*)
begin
d:= d + 1; СТЕК [d]:= v; num:= num + 1;
wgn [v]:= num;
for u [v] do
if wgn [u] = 0 then ЦИКЛ (u)
else
if (u СТЕК [d - 1]) and (wgn [v] > wgn [u]) then
(* {v, u} замыкает новый цикл *)
(* Выписать цикл с вершинами: *)
writeln(СТЕК [d], СТЕК [d - 1], ..., СТЕК [с]) (*, где СТЕК [с] = u *);
d:=d - 1 (* использованная вершина v удаляется из стека (после окончания цикла for)*)
end; (* ЦИКЛ *)
begin (*главная программа*)
for v V do wgn [v]:=0; num:= 0; (* инициализация *)
d:= 0; СТЕК [0]:= 0; (* d = число элементов в стеке*)
for v V do
if wgn [v] =0 then ЦИКЛ (v)
end.
Оценим теперь вычислительную сложность этого алгоритма. Отметим сначала, что общее число шагов, не считая затрат на выписывание циклов как и во всех алгоритмах, основанных на поиске в глубину, имеет порядок O (n + m). К этому следует прибавить суммарную длину всех циклов. Эта длина не превосходит (m-n+1)n, что дает общую сложность алгоритма O (nm + n) .
5.2. Определение всех циклов в графе
Введем для произвольных множеств A и B операцию
А В = (А В) \ (А В).
Множество A B будем называть симметрической разностью множеств A и В.
Приведем без доказательства следующую важную теорему о фундаментальном множестве циклов.
Теорема 5.1. Пусть G = V, Е - связный неориентированный граф и V, Т - его стягивающее дерево. Произвольный цикл графа G можно однозначно представить как симметрическую разность некоторого числа фундаментальных циклов.
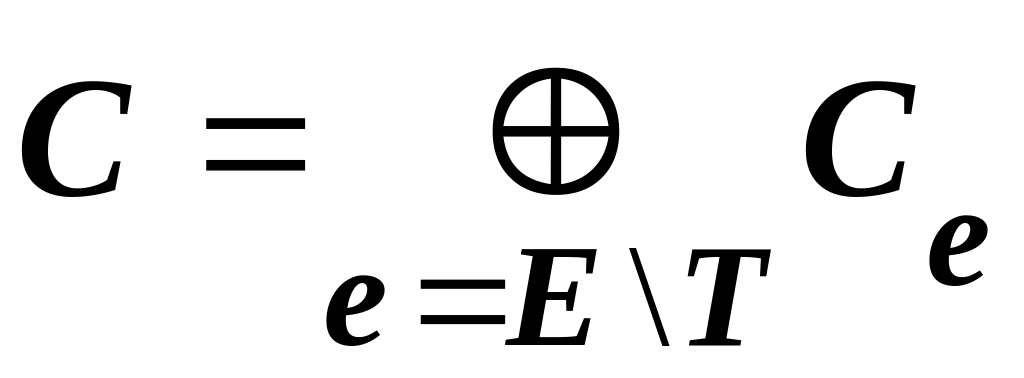
Эта теорема дает нам простой алгоритм поиска всех циклов в графе. Для этого необходимо перебрать все возможные сочетания фундаментальных циклов, имеющих хотя бы одно общее ребро. Четное количество общих ребер дает пустое ребро, а нечетное - сохраняет это ребро в результате операции. В полученном результате следует разделить так называемые “псевдоциклы”, состоящие из нескольких простых циклов соединенных общей вершиной и исключить повторяющиеся циклы.