
- •Методические указания и контрольные задания по высшей математике для студентов-заочников экономических специальностей агау
- •Общие методические указания
- •Указания к выполнению контрольной работы № 1 Тема 1. Аналитическая геометрия на плоскости
- •Тема 2. Векторная алгебра и аналитическая геометрия в пространстве.
- •Тема 3. Элементы линейной алгебры
- •Глава 2, с. 42 пример 2.1, с.46 примеры 2.2 – 2.3, с.49 пример 2.4.
- •Тема 4. Введение в анализ.
- •Тема 5. Производная и дифференциал функции.
- •Тема 6. Приложения производной.
- •Тема 7. Функции нескольких переменных.
- •Указания к выполнению контрольной работы №2 Тема 8. Неопределенный интеграл.
- •Тема 9. Определенный интеграл.
- •Тема 10. Дифференциальные уравнения.
- •Тема 11. Ряды.
- •Указания к выполнению контрольной работы №3. Тема 12. Повторные независимые испытания.
- •Тема 13. Случайные величины и их характеристики.
- •Тема 14. Элементы линейного программирования.
- •Графический метод решения.
- •Аналитический метод решения.
- •Задачи для контрольных работ Контрольная работа №1
- •Контрольная работа №2.
- •Контрольная работа №3.
- •Литература
Тема 14. Элементы линейного программирования.
[7] c. 71 – 75 задачи 1- 3.
[10] с. 540 §3, c. 542 пример 1.
[13] c. 419 §29, с. 421 – 424 №29.1 – 29.4.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 29. Предприятие имеет возможность приобрести не более 20 трехтонных и не более 18 пятитонных автомашин. Отпускная цена трехтонного грузовика 4 млн. руб., пятитонного – 5 млн. руб. Сколько нужно приобрести автомашин каждой марки, чтобы их суммарная грузоподъемность была максимальной, если для приобретения автомашин выделено 150 млн. рублей? Задачу решить графическим и аналитическим методами.
Решение.
Пусть приобретено трехтонных и пятитонных автомашин. По условию задачи имеем систему ограничений:
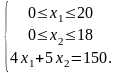
Суммарная грузоподъемность приобретенных грузовиков равна
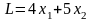 .
.
Задача состоит в определении такого решения системы ограничений, при котором линейная форма L (целевая функция) принимает наибольшее значение.
Графический метод решения.
В прямоугольной
системе координат
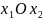 построим
многоугольник OABCD,
образованный прямыми
=
0 (OD),
=
20 (AB),
=
0 (AO),
=
18 (CD),
4
+5
=150
(BC)
и прямую 3
+5
=0
(l)
(рис.7).
построим
многоугольник OABCD,
образованный прямыми
=
0 (OD),
=
20 (AB),
=
0 (AO),
=
18 (CD),
4
+5
=150
(BC)
и прямую 3
+5
=0
(l)
(рис.7).
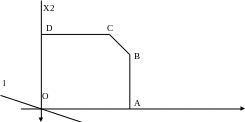
X1
Рис.7.
Системе ограничений удовлетворяют координаты точек, лежащих на пятиугольнике OABCD и внутри него. Т.к. прямые (l) и (ВС) не параллельны, то для определения оптимального решения системы ограничений, для которой линейная форма L принимает наибольшее значение, достаточно определить значения этой формы в точках A, B, C, D и из полученных чисел выбрать наибольшее. Эти точки в нашей задаче имеют следующие координаты: A(20, 0), B(20, 14), C(15, 18), D(0, 18). Подставляя координаты этих точек, определяем значения целевой функции:
L(A)=L(20; 0)=60; L(B)=L(20; 14)=130; L(C)=L(15; 18)=135; L(D)=L(0; 18)=90.
Следовательно, Lmax=L(15; 18)=135, т.е. предприятию следует приобрести 15 трехтонных и 18 пятитонных автомашин.
Аналитический метод решения.
В
систему ограничений введем дополнительные
неизвестные
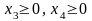 ,
чтобы она приняла следующий вид:
,
чтобы она приняла следующий вид:

Эта система имеет 3 уравнения и 4 неизвестных. Примем, например, x1, x2, x3 за базисные неизвестные, а x4 за базисное неизвестное и выразим из системы ограничений неизвестные , x1, x2, x3 через. x4. Тогда
 и
и
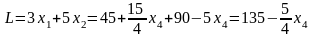 .
.
Из
последнего выражения следует, что L
принимает наибольшее значение при x4.
= 0 (т.к.
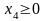 ).
При x4.
= 0 имеем: x1
= 15, x2
= 18 и L(15;
18)=135.
).
При x4.
= 0 имеем: x1
= 15, x2
= 18 и L(15;
18)=135.
Следовательно, предприятие должно приобрести 15 трехтонных и 18 пятитонных автомашин при их общей грузоподъемности 135 тонн.
Вопросы для самопроверки.
Сформулируйте основную задачу линейного программирования. Приведите примеры.
Дайте геометрическую интерпретацию основной задачи линейного программирования.
В чем суть симплекс-метода решения задач линейного программирования?
Задачи для контрольных работ Контрольная работа №1
В задачах 1 – 20 даны вершины треугольника ABC.
Определить: 1) длину стороны AB; 2) уравнения сторон AB и AС и их угловые коэффициенты; 3) внутренний угол A в радианах с точностью до 0,01; 4) уравнение высоты CD и ее длину; 5) уравнение окружности, для которой высота CD есть диаметр; 6) систему линейных неравенств, определяющих треугольник ABC.
A(-8;- 3), B(4; -12), C(8; 10).
A(-5; 7), B(7; -2), C(11; 20).
A(-12; -1), B(0; -10), C(4; 12).
A(-10; 9), B(2; 0), C(6; 22).
A(0; 2), B(12; -7), C(16; 15).
A(-9; 6), B(3; -3), C(7; 19).
A(1; 0), B(13; -9), C(17; 13).
A(-4; 10), B(8; 1), C(12; 23).
A(2; 5), B(14; -4), C(18; 18).
A(-1; 4), B(11; -5), C(15; 17).
A(-6; 8), B(6; -1), C(4; 13).
A(-2; 7), B(10; -2), C(8; 12).
A(3; 6), B(15; -3), C(13; 11).
A(-10; 5), B(2; -4), C(0; 10).
A(-4; 12), B(8; 3), C(6; 17).
A(-3; 10), B(9; 1), C(7; 15).
A(4; 1), B(16; -8), C(14; 6).
A(-7; 4), B(5; -5), C(3; 9).
A(0; 3), B(12; -6), C(10; 8).
A(-5; 9), B(7; 0), C(5; 14).
В
задачах 21
–40 даны
координаты точек A,
B,
C.
Требуется: 1) записать векторы
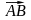 и
и
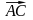 в системе орт и определить модули этих
векторов; 2) определить угол между
векторами
и
;
3) составить уравнение плоскости,
проходящей через точку С перпендикулярно
вектору
.
в системе орт и определить модули этих
векторов; 2) определить угол между
векторами
и
;
3) составить уравнение плоскости,
проходящей через точку С перпендикулярно
вектору
.
A(7; -4; 1), B(12; -3; 1), C(10; 1; 5).
A(0; -3; 3), B(5; -2; 3), C(3; 2; 7).
A(-2; -1; -2), B(3; 0; -2), C(1; 4; 2).
A(-6; 0; 0), B(-1; 1; 0), C(-3; 5; 4).
A(-2; -3; -8), B(3; -2; -8), C(1; 2; -4).
A(1; 0; -1), B(6; 1; -1), C(4; 5; 3).
A(-1; 4; 1), B(4; 5; 1), C(2; 9; 5).
A(3; -6; -3), B(8; -5; -3), C(6; -1; 1).
A(1; 0; 0), B(6; 1; 0), C(4; 5; 4).
A(2; -8; -2), B(7; -7; -2), C(5; -3; 2).
А(-1; 3; 3), В(2; 2; 1), С(0; 3; -2).
А(2; 3; -1), В(0; 4; 5), С(-2; -2; 4).
А(2; 1; 0), В(3; 0; 3), С(2; -3; 7).
А(-3; 1; 3), В(1; 7; 2), С(7; 3; 3).
А(0; 2; 1), В(4; 0; 1), С(3; -4; 2).
А(0; -2; 1), В(-2; 0; 2), С(0; 1; 0).
А(-1; 2; 1), В(-4; -3; 1), С(5; 4; 2).
А(2; 3; -1), В(-3; 4; 1), С(-2; 2; -4).
А(3; -4; 6), В(1; -2; 6), С(-3; 5; 1).
А(4; -3; 2), В(-1; 4; 3), С(6; 3; -2).
В
задачах 41 –
60 даны векторы
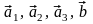 .
Показать, что векторы
.
Показать, что векторы
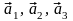 образуют базис трехмерного пространства
и найти координаты вектора
образуют базис трехмерного пространства
и найти координаты вектора
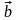 в этом базисе.
в этом базисе.
41.
 .
.
42.
 .
.
43.
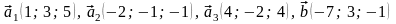 .
.
44.
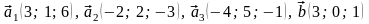 .
.
45.
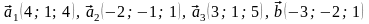 .
.
46.
 .
.
47.
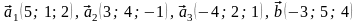 .
.
48.
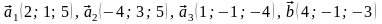 .
.
49.
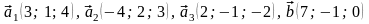 .
.
50.
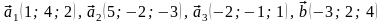 .
.
51.
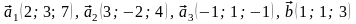 .
.
52.
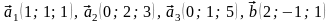 .
.
53.
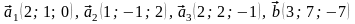 .
.
54.
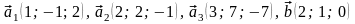 .
.
55.
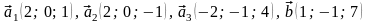 .
.
56.
 .
.
57.
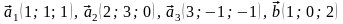 .
.
58.
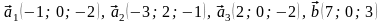 .
.
59.
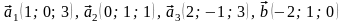 .
.
60.
 .
.
В задачах 61 – 80 систему уравнений: а) записать в матричной форме и решить ее с помощью обратной матрицы; б) решить методом Гаусса; в) решить методом Крамера.
61.
 62.
62.
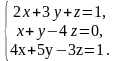
63.
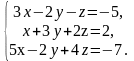 64.
64.

65.
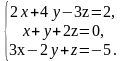 66.
66.
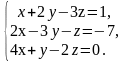
67.
 68.
68.
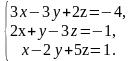
69.
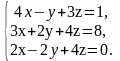 70.
70.
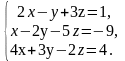
71.
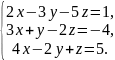 72.
72.
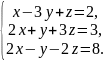
73.
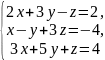 74.
74.

75.
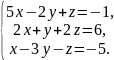 76.
76.
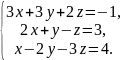
77.
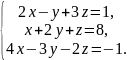 78.
78.
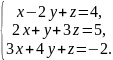
79.
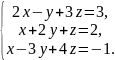 80.
80.
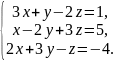
В задачах 81 – 100 вычислить указанные пределы.
81.
а)
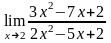 ;
б)
;
б)
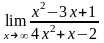 ;
;
в)
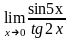 ;
г)
;
г)
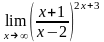 .
.
82.
а)
 ;
б)
;
б)
 ;
;
в)
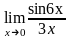 ;
г)
;
г)
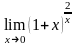 .
.
83.
а)
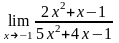 ;
б)
;
б)
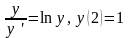 ;
;
в)
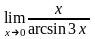 ;
г)
;
г)
 .
.
84.
а)
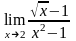 ;
б)
;
б)
 ;
;
в)
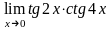 ;
г)
;
г)
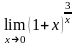 .
.
85.
а)
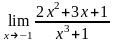 ;
б)
;
б)
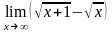 ;
;
в)
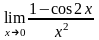 ;
г)
;
г)
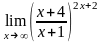 .
.
86.
а)
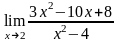 ;
б)
;
б)
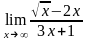 ;
;
в)
 ;
г)
;
г)
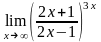 .
.
87.
а)
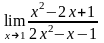 ;
б)
;
б)
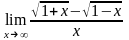 ;
;
в)
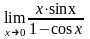 ;
г)
;
г)
 .
.
88.
а)
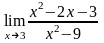 ;
б)
;
б)
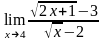 ;
;
в)
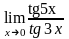 ;
г)
;
г)
 .
.
89.
а)
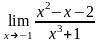 ;
б)
;
б)
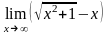 ;
;
в)
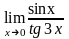 ;
г)
;
г)
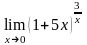 .
.
90.
а)
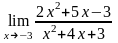 ;
б)
;
б)
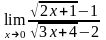 ;
;
в)
 ;
г)
;
г)
 .
.
91.
а)
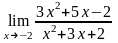 ;
б)
;
б)
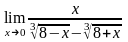 ;
;
в)
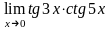 ;
г)
;
г)
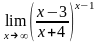 .
.
92.
а)
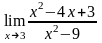 ;
б)
;
б)
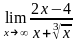 ;
;
в)
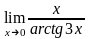 ;
г)
;
г)
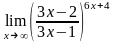 .
.
93.
а)
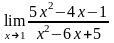 ;
б)
;
б)

в)
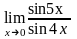 ;
г)
;
г)
 .
.
94.
а)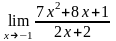 ;
б)
;
б)
 ;
;
в)
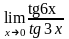 ;
г)
;
г)
 .
.
95.
а)
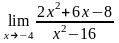 ;
б)
;
б)
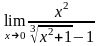 ;
;
в)
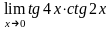 ;
г)
;
г)
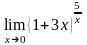 .
.
96.
а)
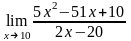 ;
б)
;
б)
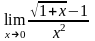 ;
;
в)
 ;
г)
;
г)
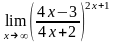 .
.
97.
а)
 ;
б)
;
б)
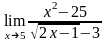 ;
;
в)
 ;
г)
;
г)
 .
.
98.
а)
 ;
б)
;
б)
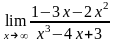 ;
;
в)
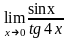 ;
г)
;
г)
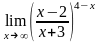 .
.
99.
а)
 ;
б)
;
б)
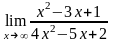 ;
;
в)
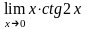 ;
г)
;
г)
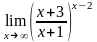 .
.
100.
а)
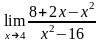 ;
б)
;
б)
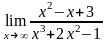 ;
;
в)
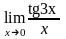 ;
г)
;
г)
 .
.
В задачах 101 – 120 определить производные функций.
101.
а)
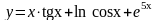 ;
б)
;
б)
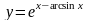 ;
;
в)
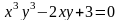 .
.
102.
а)
 ;
б)
;
б)
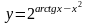 ;
;
в)
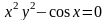 .
.
103.
а)
 ;
б)
;
б)
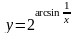 ;
;
в)
 .
.
104.
а)
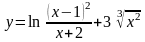 ;
б)
;
б)
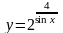 ;
;
в)
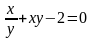 .
.
105.
а)
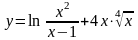 ;
б)
;
б)
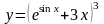 ;
;
в)
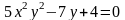 .
.
106.
а)
 ;
б)
;
б)
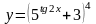 ;
;
в)
 .
.
107.
а)
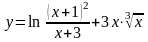 ;
б)
;
б)
 ;
;
в)
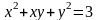 .
.
108.
а)
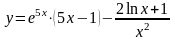 ;
б)
;
б)
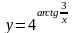 ;
;
в)
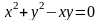 .
.
109.
а)
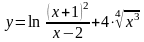 ;
б)
;
б)
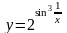 ;
;
в)
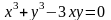 .
.
110.
а)
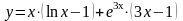 ;
б)
;
б)
 ;
;
в)
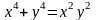 .
.
111.
а)
 ;
б)
;
б)
 ;
;
в)
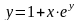 .
.
112.
а)
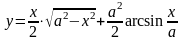 ;
б)
;
б)
 ;
;
в)
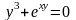 .
.
113.
а)
 ;
б)
;
б)
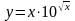 ;
;
в)
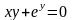 .
.
114.
а)
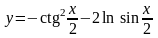 ;
б)
;
б)
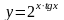 ;
;
в)
 .
.
115.
а)
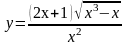 ;
б)
;
б)
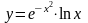 ;
;
в)
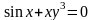 .
.
116.
а)
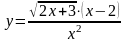 ;
б)
;
б)
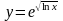 ;
;
в)
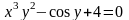 .
.
117.
а)
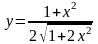 ;
б)
;
б)
 ;
;
в)
 .
.
118.
а)
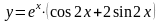 ;
б)
;
б)
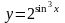 ;
;
в)
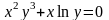 .
.
119.
а)
 ;
б)
;
б)
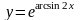 ;
;
в)
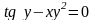 .
.
120.
а)
 ;
б)
;
б)
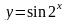 ;
;
в)
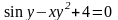 .
.
В задачах 121–140 исследовать данные функции методами дифференциального исчисления и построить их графики. Исследование функции рекомендуется проводить по следующей схеме: 1) установить область определения функции; 2) исследовать функцию на непрерывность; 3) определить, является ли данная функция четной, нечетной; 4) определить интервалы возрастания и убывания функции и точки ее экстремума; 5) определить интервалы выпуклости и вогнутости графика функции и точки перегиба; 6) определить асимптоты графика функции.
121.
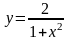 .
122.
.
122.
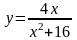 .
123.
.
123.
 .
.
124.
 125.
125.
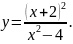 126.
126.
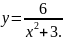
127.
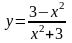 .
128.
.
128.
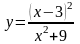 .
129.
.
129.
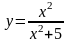 .
.
130.
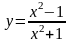 .
131.
.
131.
 .
132.
.
132.
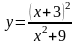 .
.
133.
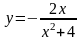 .
134.
.
134.
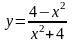 .
135.
.
135.
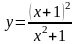 .
.
136.
 .
137.
.
137.
 .
138.
.
138.
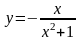 .
.
139.
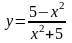 .
140.
.
140.
 .
.
141. Каковы радиус основания R и высота H открытого цилиндрического бака данного объема V, чтобы на его изготовление пошло наименьшее количество листового металла?
142. Сечение тоннеля имеет форму прямоугольника, завершенного сверху полукругом. Периметр сечения 18м. При каком радиусе полукруга площадь сечения будет наибольшей?
143. Определить
длину сторон прямоугольника наибольшей
площади, который можно вписать в эллипс
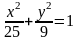 .
.
144. Определить наибольший объем цилиндра, полная поверхность которого равна S.
145. Определить наибольший объем конуса, образующая которого равна 3м.
146. Определить
размеры открытого бассейна с квадратным
дном объемом 32
 так, чтобы на облицовку его стен и дна
пошло наименьшее количество материала.
так, чтобы на облицовку его стен и дна
пошло наименьшее количество материала.
147. Сумма двух положительных чисел равна a. Каковы эти числа, если сумма их кубов будет наименьшей?
148. Два коридора шириной 2,4 м. и 1,6 м. пересекаются под прямым углом. Определить наибольшую длину лестницы, которую можно перенести горизонтально из одного коридора в другой.
149. На
параболе
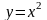 указать точку, наименее удаленную от
прямой
указать точку, наименее удаленную от
прямой
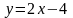 .
.
150. Из всех прямоугольников, вписанных в круг радиуса R, указать тот, который имеет наибольшую площадь.
151. В прямоугольной системе координат через точку М(2;3) проведена прямая, которая вместе с осями координат образует треугольник, расположенный в первом квадранте. Каковы должны быть отрезки, отсекаемые прямой на осях координат, чтобы площадь треугольника была наименьшей?
152. Резервуар, открытый сверху, имеет форму прямоугольного параллелепипеда с квадратным основанием. Каковы должны быть размеры резервуара, чтобы на его изготовление пошло наименьшее количество материала, если он должен вмещать 256 л. воды.
153. Требуется
вырыть яму цилиндрической формы с
круглым основанием и вертикальной
боковой поверхностью заданного объема
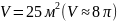 .
Каковы должны быть размеры ямы (радиус
R
и высота H),
чтобы на облицовку ее дна и боковой
поверхности пошло наименьшее количество
материала?
.
Каковы должны быть размеры ямы (радиус
R
и высота H),
чтобы на облицовку ее дна и боковой
поверхности пошло наименьшее количество
материала?
154. Равнобедренный треугольник, периметр которого равен 12, вращается вокруг основания. Найти основание а, при котором полученное тело вращения имеет набольший объем?
155. Сечение оросительного канала имеет форму равнобочной трапеции, боковые стороны которой равны меньшему основанию. При каком угле наклона боковых сторон сечение канала будет иметь наибольшую площадь?
156. Определить высоту конуса наибольшего объема, который можно вписать в шар радиуса R.
157. Из
прямоугольного листа жести размером
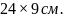 требуется изготовить открытую сверху
коробку, вырезая по углам листа равные
квадраты и загибая оставшиеся боковые
полосы под прямым углом. Каковы должны
быть стороны вырезаемых квадратов,
чтобы вместимость коробки была наибольшей?
требуется изготовить открытую сверху
коробку, вырезая по углам листа равные
квадраты и загибая оставшиеся боковые
полосы под прямым углом. Каковы должны
быть стороны вырезаемых квадратов,
чтобы вместимость коробки была наибольшей?
158. Равнобедренный треугольник, вписанный в окружность радиуса R=3, вращается вокруг основания. Найти высоту треугольника h, при котором полученное тело вращения имеет наибольший объем.
159. Требуется
изготовить полотняный шатер, имеющий
форму прямого кругового конуса заданной
вместимости

 .
Каковы должны быть размеры конуса
(радиус основания R
и высота H),
чтобы на шатер ушло наименьшее количество
полотна?
.
Каковы должны быть размеры конуса
(радиус основания R
и высота H),
чтобы на шатер ушло наименьшее количество
полотна?
160. Требуется
поставить палатку в форме правильной
четырехугольной пирамиды заданной
боковой поверхности
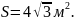 Каковы должны быть размеры палатки
(сторона основания a
и высота
H),
чтобы вместимость палатки была наибольшей?
Каковы должны быть размеры палатки
(сторона основания a
и высота
H),
чтобы вместимость палатки была наибольшей?
В задачах 161 – 170 исследовать на экстремум функцию z = f(x,y).
161.
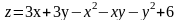 .
.
162.
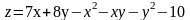 .
.
163.
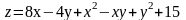 .
.
164.
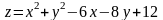 .
.
165.
 .
.
166.
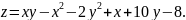
167.
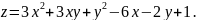
168.
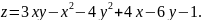
169.
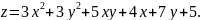
170.

В задачах 171 – 180 определить наибольшее и наименьшее значения функции z = f(x,y) в данной замкнутой области.
171.
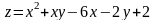 в прямоугольнике
в прямоугольнике
 .
.
172.
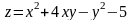 в треугольнике, ограниченном осями OX
и OY
и прямой
в треугольнике, ограниченном осями OX
и OY
и прямой
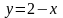 .
.
173.
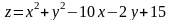 в прямоугольнике
в прямоугольнике
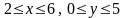 .
.
174.
в области, ограниченной параболой
 и осью Ох.
и осью Ох.
175.
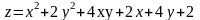 `в
квадрате
`в
квадрате
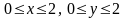 .
.
176.
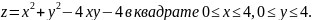
177.
.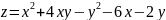 в треугольнике,
ограниченном осями координат Ох
и Оу
и прямой
в треугольнике,
ограниченном осями координат Ох
и Оу
и прямой

178.
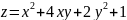 в квадрате
в квадрате
179.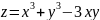 в квадрате
в квадрате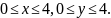
180.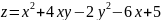 в треугольнике,
ограниченном осями координат Ох
и Оу
и прямой
в треугольнике,
ограниченном осями координат Ох
и Оу
и прямой

