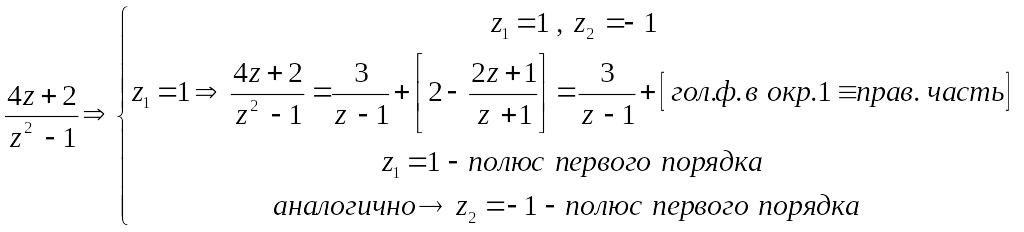- •1. Поле комплексных чисел. Действительная и мнимая части, модуль и аргумент комплексного числа.
- •2. Формула Муавра, корень n-ой степени из комплексного числа. Расширенная комплексная плоскость.
- •4. Ряды функций комплексного переменного: равномерная сходимость, признак Вейерштрасса.
- •Равномерная сходимость:
- •5. Степенной ряд: теорема Абеля, формула Коши-Адамара, область сходимости.
- •6. Функции комплексного переменного: предел, непрерывность и их связь с функциями действительного переменного.
- •7. Дифференцируемые и голоморфные функции комплексного переменного. Условия Коши-Римана.
- •8. Геометрический смысл аргумента и модуля производной. Понятие конформного отображения.
- •9. Интеграл функции комплексного переменного. Первообразная голоморфной функции: локальная первообразная, первообразная вдоль пути, формула Ньютона-Лейбница.
- •10. Гомотопия путей с общими концами и замкнутых путей. Теорема Коши.
- •11. Глобальная теорема существования первообразной для голоморфной функции в односвязной области.
- •12. Теорема Коши для многосвязной области. Интегральная формула Коши.
- •13. Теорема Коши для многосвязной области.
- •15. Свойства голоморфных функций. Гармонические функции. Интегральная формула Коши для производных голоморфной функции.
- •16. Интегральная формула Коши для производных голоморфной функции.
- •17. Теорема Мореры. Функции, голоморфные в смысле Коши, Римана и Вейерштрасса. Теорема Вейерштрасса о рядах голоморфных функций.
- •18. Нули в голоморфной функции и их кратность. Теорема единственности голоморфной функции.
- •19. Аналитическое продолжение: принцип аналитического продолжения.
- •20. Аналитическое продолжение через границу области: лемма о непрерывной продолжении, принцип симметрии Римана-Шварца. Аналитическая функция в смысле Вейерштрасса.
- •21. Ряд Лорана: теорема Лорана, правильная и главная части, теорема единственности, неравенства Коши.
- •2 2. Изолированные особые точки однозначного характера. Теорема Сохоцкого, теорема Пикара.
- •23. Целые и мероморфные функции: теорема Вейерштрасса и теорема Миттаг-Леффлера.
- •24. Изолированные особые точки многозначного характера
- •25. Основные элементарные многозначные функции.
- •26. Вычеты: определение, теорема Коши. Теорема о полной сумме вычетов.
- •27. Интеграл типа Коши.
- •28. Логарифмический вычет. Принцип аргумента и теорема Руше.
- •29. Принцип максимума модуля. Лемма Шварца.
- •30. Теорема Монтеля (принцип компактности). Теорема Гурвица.
21. Ряд Лорана: теорема Лорана, правильная и главная части, теорема единственности, неравенства Коши.
Степенные ряды с целыми показателями степеней называются рядами Лорана. В качестве суммы ряда Лорана ряда можно взять один из пределов
![]()

![]()
Теорема 15. Голоморфная в открытом кольце функция разлагается в этом кольце в ряд Лорана.
Доказательство. Пусть функция
![]() голоморфна в кольце
голоморфна в кольце
![]() .
По произвольной точке
из кольца выберем числа
.
По произвольной точке
из кольца выберем числа
![]() так, чтобы
так, чтобы
![]() .
Тогда согласно ИФК имеем
.
Тогда согласно ИФК имеем

Разложение в степенной ряд для
![]() дословно повторяет доказательство
теоремы 9, так как в этом случае
дословно повторяет доказательство
теоремы 9, так как в этом случае
![]() .
Таким образом,
.
Таким образом,
![]() Аккуратно запишем разложение в степенной
ряд для
.
Аккуратно запишем разложение в степенной
ряд для
.

Отсюда имеем соотношение
![]() .Теорема
доказана.
.Теорема
доказана.

2 2. Изолированные особые точки однозначного характера. Теорема Сохоцкого, теорема Пикара.
Изолированная особая точка в зависимости от количества слагаемых в главной части считается:
устранимой изолированной особой точкой, если главная часть отсутствует,
полюсом порядка , если главная часть содержит только конечное число слагаемых и - показатель наименьшей отрицательной степени
 в главной части,
в главной части,существенно особой точкой, если в главной части бесконечно много слагаемых.
Примеры.

Если в окрестности полюса и устранимой особой точки поведение функции достаточно регулярно (существует предел), то совсем иначе устроена функция в окрестности существенно особой точки
Теорема 1. (Ю.Сохоцкий – Ф. Казорати)
Если
![]() является существенно особой точкой
функции
, то для любого конечного или бесконечного
найдется последовательность точек
является существенно особой точкой
функции
, то для любого конечного или бесконечного
найдется последовательность точек
![]() сходящаяся к особой точке
и такая, что
сходящаяся к особой точке
и такая, что
![]()
Теорема 2. ( Э.Пикар, 1879) В любой окрестности существенно особой точки любая функция принимает все значения, за исключением, быть может, одного.
Доказательство теоремы 1. Так как в
окрестности существенно особой точки
функция неограниченна, то теорема верна
при
![]() .
Пусть теперь
- конечное число. Предположим противное:
найдется проколотая окрестность особой
точки . функция не принимает значения
.
Введем функцию по формуле
.
Пусть теперь
- конечное число. Предположим противное:
найдется проколотая окрестность особой
точки . функция не принимает значения
.
Введем функцию по формуле
![]() ограничена в окрестности особой точки.
Чего не может быть, так как при таком
построении сущесвенно особая точка не
может стать устранимой особой точкой.
Теорема доказана.
ограничена в окрестности особой точки.
Чего не может быть, так как при таком
построении сущесвенно особая точка не
может стать устранимой особой точкой.
Теорема доказана.
23. Целые и мероморфные функции: теорема Вейерштрасса и теорема Миттаг-Леффлера.
До сих пор мы изучали функции, которые являлись голоморфными в некоторой открытой части комплексной плоскости. Теперь исследуем свойства голомофных на всей комплексной плоскости. Голоморфная на всей комплексной плоскости функция называется целой функцией. Приведем некоторые свойства целой функции: 1) Разлагается в ряд Тейлора с бесконечным радиусом сходимости. 2) Нули изолированы без конечных предельных точек.