15. Свойства голоморфных функций. Гармонические функции. Интегральная формула Коши для производных голоморфной функции.

• Из следует, что внутренние значения голоморфной функции можно находить (восстановить) по значениям на границе 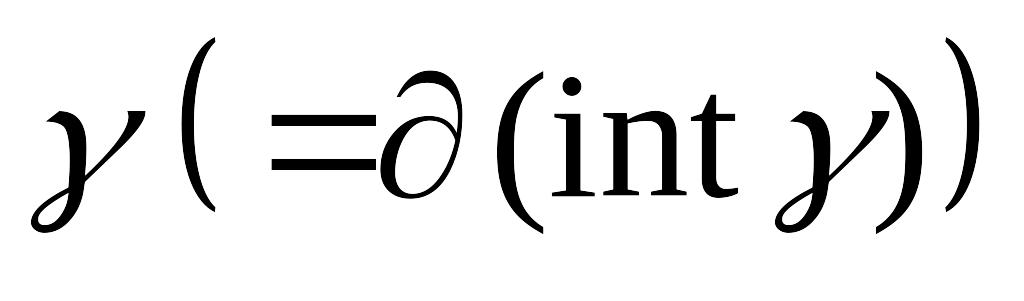. Подобные проблемы восстановления функции по граничным значениям возникают в теории краевых задач.

• Вспомним, что рациональная функция представляется в виде суммы простейших дробей. К примеру, когда 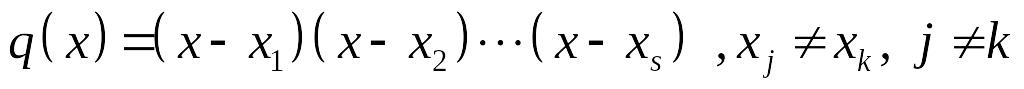, то справедливо разложение . Тогда интегральная формула Коши представляет полный аналог разложения рациональной функции (роль играет ). Следовательно, голоморфная функция обладает многими свойствами рациональных функций.

• Поскольку интегральную формулу Коши можно по параметру неограниченное число раз дифференцировать, то голоморфная функция бесконечно дифференцируема.

• Интегральная формула Коши вместо вычисления интеграла разрешает вычислять значения голоморфной функции или значения ее производной. Действительно

16. Интегральная формула Коши для производных голоморфной функции.

Теорема Коши говорит о равенстве интегралов . Поэтому по своему желанию можно вычислять либо левую, либо правую часть равенства. Обычно выбирают ту, которая легче находится. Применим подобные рассуждения для вычисления интеграла , когда - голоморфная на всей комплексной плоскости функция, а - произвольный замкнутый контур

• Если точка то подынтегральная функция будет голоморфной в некотором - раздутии . Тогда по теореме 7 .

• Если точка то подынтегральная функция будет голоморфной в некоторой проколотой окрестности точки . Каждая окружность с центров в точке гомотопна контуру , так как, не затрагивая точку , можно контур деформировать в указанную окружность. По теореме 6 имеем . Поскольку левая часть последнего равенства не зависит от , то можно записать предельное соотношение

Таким образом, надо найти правую часть последнего равенства.

Следовательно, при имеем формулу , которую называют интегральной формулой Коши. Продифференцировав по обе части приведенной формулы, получим представление для производной . Можно продолжить дифференцирование.

Интегральная формула Коши вместо вычисления интеграла разрешает вычислять значения голоморфной функции или значения ее производной. Действительно

17. Теорема Мореры. Функции, голоморфные в смысле Коши, Римана и Вейерштрасса. Теорема Вейерштрасса о рядах голоморфных функций.

Теорема (Морера ( Th M)). Если функция непрерывна в области и интеграл от нее по границе любого треугольника равен нулю, то .

Доказательство. Для любой точки из области построим круг . Введем функцию по формуле . Покажем, что . Поэтому рассмотрим соответствующее приращение функции Тогда отношение приращений примет вид