11. Глобальная теорема существования первообразной для голоморфной функции в односвязной области.

12. Теорема Коши для многосвязной области. Интегральная формула Коши.

Теорема 7. (Коши для односвязной области) Интеграл от голоморфной в односвязной области функции вдоль любого замкнутого контура равен нулю.

Кстати, замкнутые кривые часто представляют границы областей. Поэтому справедлива

Теорема 8. (Коши для многосвязных областей)

Пусть . Если граница - связное множество, то -раздутие

подобласти представляет односвязную область и - замкнутый контур в этом раздутии. Из теоремы 7 для этого раздутия следует, что . (ч.т.д.)

Теорема Коши говорит о равенстве интегралов . Поэтому по своему желанию можно вычислять либо левую, либо правую часть равенства. Обычно выбирают ту, которая легче находится. Применим подобные рассуждения для вычисления интеграла , когда - голоморфная на всей комплексной плоскости функция, а - произвольный замкнутый контур

• Если точка то подынтегральная функция будет голоморфной в некотором - раздутии . Тогда по теореме 7 .

• Если точка то подынтегральная функция будет голоморфной в некоторой проколотой окрестности точки . Каждая окружность с центров в точке гомотопна контуру , так как, не затрагивая точку , можно контур деформировать в указанную окружность. По теореме 6 имеем 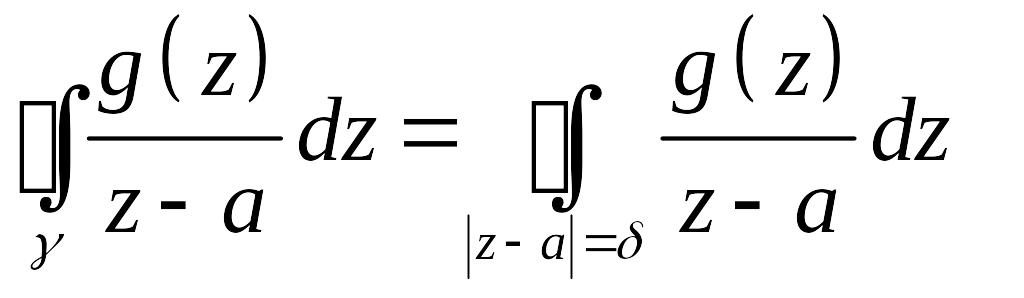. Поскольку левая часть последнего равенства не зависит от , то можно записать предельное соотношение

Таким образом, надо найти правую часть последнего равенства.

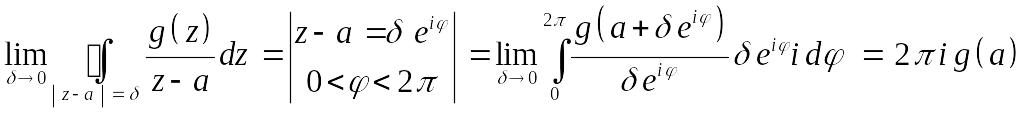
Следовательно, при имеем формулу , которую называют интегральной формулой Коши. Продифференцировав по обе части приведенной формулы, получим представление для производной . Можно продолжить дифференцирование.

13. Теорема Коши для многосвязной области.

Пусть . Если граница - связное множество, то -раздутие

подобласти представляет односвязную область и - замкнутый контур в этом раздутии. Из теоремы 7 для этого раздутия следует, что .

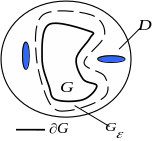
Если граница - несвязна, то достраиваем мосты, соединяющие несвязные компоненты границы. Причем по одному и тому же мосту производится обход дважды и в разных направлениях. С помощью построенных мостов можно получить замкнутый контур, лежащий в односвязной области. Затем применим теорему 7. Откуда получаем теорему 8 из теоремы7. На рисунке ниже кольцо подобласть области и его граница состоит из двух окружностей. Запомните: граница считается ориентированной, то есть она ориентирована так, что при ее обходе область остается слева. Эти окружности соединяем мостом и обходим его дважды в разных направлениях. Тогда можно получить ориентированную замкнутую линию гомотопную в области контуру (смотри рисунок). Контур можно считать принадлежащим некоторой односвязной области и применить теорему 7 к этой области. Тогда из теоремы 7 будет следовать теорема 8, так как интегралы по дважды обходимому мосту взаимно уничтожаются.

П ояснения к данному рисунку даны выше.

На рисунке не отображена ориентация границы .

Покажите: как надо деформировать в области границу с двойным обходом моста, чтобы получить контур .

_{14. Ряд Тейлора, теорема единственности, неравенства Коши. Теорема Лиувилля. (+доказать теорему Лиувилля)}

Теорема 9.

Упражнение 15. Сформулируйте словесную формулировку теоремы 9.

Замечание для информативности. В теореме 9 разложение осуществляется в некотором круге . То есть разложение локально, так как нет оценки радиуса .

Вопрос для творческих натур. Анализируя доказательство теоремы 9, попробуйте найти максимально возможный радиус .

Доказательство теоремы 9. 1 шаг. Разложение простейшей дроби вида .

2 шаг. Разложение голомофной функции в ряд Тейлора в окрестности фиксированной точки. Пусть - фиксированная точка из области . Выберем круг с центром в точке так, чтобы .

По интегральной формуле Коши найдем значение функции в произвольной точке круга . Теперь используем результат первого шага. , так как выполняется неравенство .

Обе части последнего равенства проинтегрируем согласно интегральной формуле Коши

Отсюда следует, что , где коэффициенты

Теорема 9 доказана.

Уточним теорему 9 в следующем направлении.

Теорема 10. Указанное в теореме 9 разложение единственно.

Доказательство. Допустим , что в круге функция разлагается в ряды и . Надо показать, что . К примеру, . Точно также имеем . Дальше по индукции…Теорема 10 доказана.