6. Функции комплексного переменного: предел, непрерывность и их связь с функциями действительного переменного.
Рассматривая
вопрос непрерывности функции комплексного
переменного на самом деле мы приходим
к вопросам рассмотрения непрерывности
двух функций вещественного переменного
u(x,y)
и v(x,y)
на плоскости
.
7. Дифференцируемые и голоморфные функции комплексного переменного. Условия Коши-Римана.
8. Геометрический смысл аргумента и модуля производной. Понятие конформного отображения.
Если не предполагать голоморфности, то для приращения имеем соотношения
Поскольку
,
то
.
В результате имеем
,
где
В случае голоморфности с учетом
соотношении Коши-Римана приращение
функции примет вид
.Таким
образом,
приращение голоморфной функции «почти» пропорционально приращению
,приращение функции - «почти» линейная комбинация приращении
.
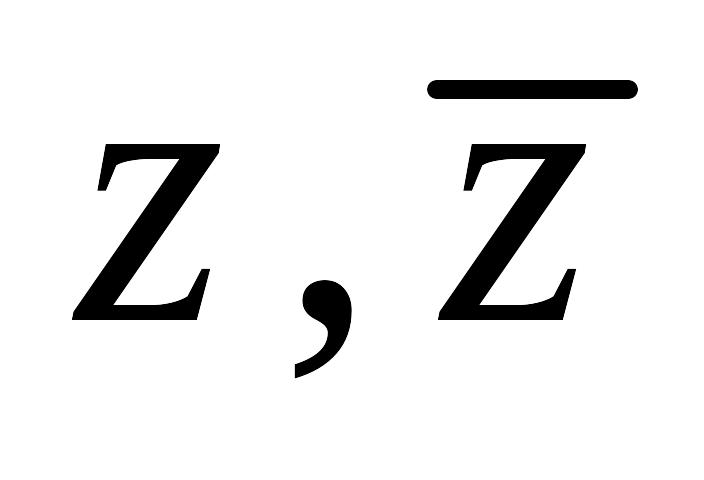Здесь «почти» означает с точностью до
.
Заметим, что
,
поэтому
.
Применяя к обеим частям последнего
приближенного равенства сначала операцию
модуль, затем аргумент комплексного
числа имеем
геометрически означает локальное
растяжение в
раз, если
.
Случай
соответствует сжатию. Таким образом,
модуль производной означает коэффициент
локального растяжения или сжатия.
геометрически означает локальный
поворот против часовой стрелки на один
и тот же угол
,
то есть разные вектора
,
начинающиеся в точке
,
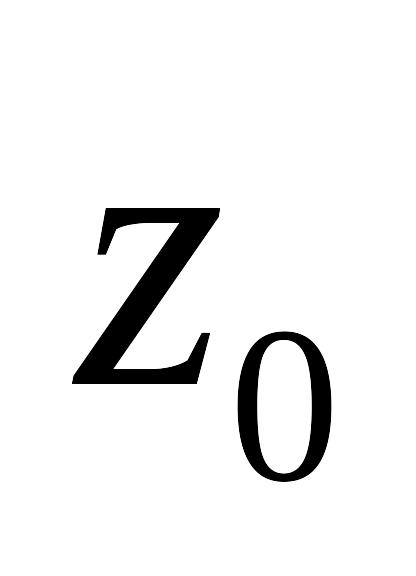поворачиваются на один и тот же угол.
Таким образом,
означает на какой угол надо повернуть
,
чтобы получить направление соответствующее
.
9. Интеграл функции комплексного переменного. Первообразная голоморфной функции: локальная первообразная, первообразная вдоль пути, формула Ньютона-Лейбница.
10. Гомотопия путей с общими концами и замкнутых путей. Теорема Коши.
Кривой или путём на
комплексной плоскости 
называется
отображение вида 
.
Особо стоит отметить, что при таком
определении можно конкретизировать не
только вид кривой,
который будет зависеть от аналитических
свойств функции 
,
но и её направление.
Для примера, функции
и 
будут
определять одинаковую по виду кривую,
но проходимую в противоположных
направлениях.
Кривые 
и 
называются гомотопными,
если существует кривая 
,
зависящая от параметра 
таким
образом, что 
и 
.
Теорема 6. (Коши) Интеграл от
голоморфной в области
вдоль любых гомотопных в
кривых принимает одно и то же значение.
Краткая формулировка:
Здесь и всюду в дальнейшем
будет обозначать класс голоморфных в
функций. Приведем различные эквивалентные
формулировки теоремы Коши. Как всегда
означает границу области
.
Когда граница
- связное множество, то будем говорить,
что
- односвязная область.
Теорема 7. (Коши для односвязной области) Интеграл от голоморфной в односвязной области функции вдоль любого замкнутого контура равен нулю.
Кстати, замкнутые кривые часто представляют границы областей. Поэтому справедлива
Пусть
.
Доказывать надо только для незамкнутых
контуров. 
Рассмотрим
замкнутый контур
,
где
- совпадает с контуром
,
только его ориентация изменена. Тогда
найдется односвязная подобласть
области
,
которая содержит замкнутый контур
.
Из теоремы 7, примененной для односвязной
подобласти
,
следует, что
.
Отсюда получаем
.
Что и доказывает теорему 6.