
- •1. Поле комплексных чисел. Действительная и мнимая части, модуль и аргумент комплексного числа.
- •2. Формула Муавра, корень n-ой степени из комплексного числа. Расширенная комплексная плоскость.
- •4. Ряды функций комплексного переменного: равномерная сходимость, признак Вейерштрасса.
- •Равномерная сходимость:
- •5. Степенной ряд: теорема Абеля, формула Коши-Адамара, область сходимости.
- •6. Функции комплексного переменного: предел, непрерывность и их связь с функциями действительного переменного.
- •7. Дифференцируемые и голоморфные функции комплексного переменного. Условия Коши-Римана.
- •8. Геометрический смысл аргумента и модуля производной. Понятие конформного отображения.
- •9. Интеграл функции комплексного переменного. Первообразная голоморфной функции: локальная первообразная, первообразная вдоль пути, формула Ньютона-Лейбница.
- •10. Гомотопия путей с общими концами и замкнутых путей. Теорема Коши.
- •11. Глобальная теорема существования первообразной для голоморфной функции в односвязной области.
- •12. Теорема Коши для многосвязной области. Интегральная формула Коши.
- •13. Теорема Коши для многосвязной области.
- •15. Свойства голоморфных функций. Гармонические функции. Интегральная формула Коши для производных голоморфной функции.
- •16. Интегральная формула Коши для производных голоморфной функции.
- •17. Теорема Мореры. Функции, голоморфные в смысле Коши, Римана и Вейерштрасса. Теорема Вейерштрасса о рядах голоморфных функций.
- •18. Нули в голоморфной функции и их кратность. Теорема единственности голоморфной функции.
- •19. Аналитическое продолжение: принцип аналитического продолжения.
- •20. Аналитическое продолжение через границу области: лемма о непрерывной продолжении, принцип симметрии Римана-Шварца. Аналитическая функция в смысле Вейерштрасса.
- •21. Ряд Лорана: теорема Лорана, правильная и главная части, теорема единственности, неравенства Коши.
- •2 2. Изолированные особые точки однозначного характера. Теорема Сохоцкого, теорема Пикара.
- •23. Целые и мероморфные функции: теорема Вейерштрасса и теорема Миттаг-Леффлера.
- •24. Изолированные особые точки многозначного характера
- •25. Основные элементарные многозначные функции.
- •26. Вычеты: определение, теорема Коши. Теорема о полной сумме вычетов.
- •27. Интеграл типа Коши.
- •28. Логарифмический вычет. Принцип аргумента и теорема Руше.
- •29. Принцип максимума модуля. Лемма Шварца.
- •30. Теорема Монтеля (принцип компактности). Теорема Гурвица.
1. Поле комплексных чисел. Действительная и мнимая части, модуль и аргумент комплексного числа.
Комплексное число – это
матрица специального вида
![]() .
Для дальнейших рассуждений удобно
преобразовать эту матрицу в виде линейной
комбинации двух фиксированных матриц.
.
Для дальнейших рассуждений удобно
преобразовать эту матрицу в виде линейной
комбинации двух фиксированных матриц.
![]()
Единичная матрица
![]() принадлежит множеству
принадлежит множеству
![]() ,
поэтому сответствует действительному
числу
,
поэтому сответствует действительному
числу
![]() и часто будем называть ее просто единицей.
Вторая матрица
и часто будем называть ее просто единицей.
Вторая матрица
![]() совпадает с матрицей
совпадает с матрицей
![]() ,
которая введена в теореме 1 и в дальнейшем
будет называться мнимой единицей.. Итак,
справедливо
,
которая введена в теореме 1 и в дальнейшем
будет называться мнимой единицей.. Итак,
справедливо
У тверждение
1. Произвольное
комплексное число представляет собой
линейную комбинацию единицы и мнимой
единицы, то есть комплексное число имеет
вид
тверждение
1. Произвольное
комплексное число представляет собой
линейную комбинацию единицы и мнимой
единицы, то есть комплексное число имеет
вид
![]() или
просто
или
просто
![]() .
Надо помнить, что коэффициенты линейной
комбинации действительные числа.
Коэффициент при единице называется
реальной частью комплексного числа, а
коэффициент при мнимой единице – мнимой
частью комплексного числа.
.
Надо помнить, что коэффициенты линейной
комбинации действительные числа.
Коэффициент при единице называется
реальной частью комплексного числа, а
коэффициент при мнимой единице – мнимой
частью комплексного числа.
2. Формула Муавра, корень n-ой степени из комплексного числа. Расширенная комплексная плоскость.


Ко́мпле́ксная плоскость— это
двумерное вещественное
пространство ![]() ,
которое изоморфно полю
комплексных чисел
,
которое изоморфно полю
комплексных чисел ![]() .
.
Сфе́ра Ри́мана — риманова
поверхность, естественная
структура на расширенной комплексной
плоскости ![]() ,
являющаяся комплексной проективной
прямой
,
являющаяся комплексной проективной
прямой ![]() .
.
Результатом компактификации комплексной плоскости является расширенная комплексная плоскость — комплексная плоскость, дополненная бесконечно удалённой точкой, изоморфная комплексной сфере.
Стереографическая проекция — центральная проекция, отображающая двумерную сферу (с одной выколотой точкой) на плоскость.
3. Последовательности комплексных чисел и их пределы. Ряды комплексных чисел. Функции комплексного переменного: предел, непрерывность. (+смотреть вопрос 6)




4. Ряды функций комплексного переменного: равномерная сходимость, признак Вейерштрасса.
![]()


Пусть
задана последовательность комплекснозначных
функций на множестве ![]() ,
включённом в d-мерное евклидово
пространство
,
включённом в d-мерное евклидово
пространство ![]() .
.
![]()
Равномерная сходимость:
Существует
функция ![]() такая,
что:
такая,
что: ![]()
Факт
равномерной сходимости последовательности ![]() к
функции
к
функции ![]() записывается:
записывается: ![]()
5. Степенной ряд: теорема Абеля, формула Коши-Адамара, область сходимости.
![]() --
степенной ряд
--
степенной ряд
![]() -- степенной ряд
-- степенной ряд
При ![]() любой
степенной ряд сходится.
любой
степенной ряд сходится.
Теорема
(Абеля): пусть
сходится
в точке ![]() ,
тогда данный ряд сходится в любой точке,
что
,
тогда данный ряд сходится в любой точке,
что ![]()
Доказательство:
пусть ![]() сходится:
сходится: ![]()
Пусть
теперь
. Тогда 
Пусть 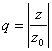 ,
причём
,
причём ![]() ,
тогда
,
тогда ![]()
Ряд ![]() сходится
как геометрическая прогрессия с
показателем меньше 1. Тогда по признаку
сравнения наш ряд сходится
сходится
как геометрическая прогрессия с
показателем меньше 1. Тогда по признаку
сравнения наш ряд сходится
Следствие: для
![]() ,
что
,
что 
![]() --
радиус сходимости степенного ряда.
--
радиус сходимости степенного ряда. ![]() --
круг сходимости степенного ряда
--
круг сходимости степенного ряда
Теорема10
(Коши-Адамара): рассмотрим степенной
ряд
,
тогда 
Пусть ![]() ,
тогда можно рассмотреть 3 случая:
,
тогда можно рассмотреть 3 случая: 
