Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесская государственная академия строительства и архитектуры

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Виш.мат.docx

Скачиваний:

Добавлен:

01.03.2025

Размер:

521.2 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

Бинарные арифметические операции

По самому определению: функция - это правило, по которому каждому элементу из области определения X соответствует единственный элемент из области значений Y. При этом области определений и значений тоже задаются для каждой функции.

Область определения и область значений функции. В элементарной математике изучаются функции только на множестве действительных чисел R.Это значит, что аргумент функции может принимать только те действительные значения, при которых функция определена, т.e. она также принимает только действительные значения. Множество X всех допустимых действительных значений аргумента x, при которых функция y = f ( x )определена, называется областью определения функции. Множество Y всех действительных значений y, которые принимает функция, называетсяобластью значений функции. Теперь можно дать более точное определение функции: правило (закон) соответствия между множествами X и Y, по которому для каждого элемента из множества X можно найти один и только один элемент из множества Y, называется функцией.

Из этого определения следует, что функция считается заданной, если:

- задана область определения функции X ;

- задана область значений функции Y ;

- известно правило ( закон ) соответствия, причём такое, что для каждого

значения аргумента может быть найдено только одно значение функции.

Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Предел функции является обобщением понятия предела последовательности: изначально под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.

Окрестностное определение по Коши

Значение называется пределом (предельным значением) функции в точке , если для любой окрестности точки существует выколотая окрестность точки такая, что образ этой окрестности лежит в . Фундаментальное обоснование данного определения предела можно найти в статье Предел вдоль фильтра.

Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.

Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения.

Классификация точек разрыва функции

Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке

Существуют левосторонний предел и правосторонний предел ;
Эти односторонние пределы конечны.

Рассмотрим функцию , определенную на некотором промежутке . Функция непрерывна в точке , если предел функции в точке равен значению функции в этой точке, .

Теорема 1. Сумма непрерывных функций есть функция непрерывная. Доказательство. Пусть функции и непрерывны в точке a. Тогда

Согласно свойству пределов функций существование пределов функций и гарантирует существование предела их суммы. При этом

что и требовалось доказать. Свойство. Сумма конечного числа непрерывных функций есть функция непрерывная. Доказательство. Каждую пару непрерывных функций можно заменить одной непрерывной функцией. Затем каждую пару полученных непрерывных функций можно заменить одной непрерывной функцией. В конечном итоге останется одна непрерывная функция.

Теорема 2. Произведение непрерывных функций есть функция непрерывная. Свойство. Произведение конечного числа непрерывных функций есть функция непрерывная. Теорема 3. Частное от деления непрерывных функций есть функция непрерывная – за исключением точек, в которых знаменатель обращается в нуль. Доказательство теорем 2 и 3 по своей сути не отличается от доказательства теоремы 1 и предоставляется читателю.

Теорема 4. Любая элементарная функция непрерывна в области своего определения. Для доказательства этой теоремы нужно показать, что для любого числа a из области определения элементарной функции выполняется условие

Продемонстрируем справедливость теоремы на некоторых конкретных примерах.

Пусть 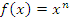, где n – целое положительное число. Тогда

Первый член в правой части этого равенства представляет собой бесконечно малую функцию при x → a и, следовательно,

Покажем, что показательная функция 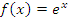является непрерывной в каждой точке a. Действительно,

Теорема 5. Пусть функция непрерывна на промежутке [a,b] и принимает на его концах значения разных знаков. Тогда на этом промежутке существует такая точка c, в которой . Действительно, непрерывность функции на некотором промежутке означает отсутствие скачков функции на этом промежутке. Другими словами, принимает все значения, заключенные между ее минимальным и максимальным значениями на промежутке [a,b], одним из которых является нулевое значение. Отметим, что теорема 5 лежит в основе численных методов решения уравнений.

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке

Таблица производных некоторых функций

Основная статья: Таблица производных