Необходимость

Пусть система совместна. Тогда существуют числа   такие, что  . Следовательно, столбец   является линейной комбинацией столбцов   матрицы  . Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что  .

24

Достаточность

Пусть  . Возьмем в матрице   какой-нибудь базисный минор. Так как  , то он же и будет базисным минором и матрицы  . Тогда согласно теореме о базисном миноре последний столбец матрицы   будет линейной комбинацией базисных столбцов, то есть столбцов матрицы  . Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы  .

25

Однородные системы

Однородной системой линейных уравнений называется система вида:

Нулевое решение   системы (1) называется тривиальным решением.

Однородные системы всегда совместны, т.к. всегда существует тривиальное решение.

Если существует любое ненулевое решение системы, то оно называется нетривиальным.

Решения однородной системы обладают свойством линейности:

Теорема (о линейном решении однородных систем). Пусть   — решения однородной системы (1),   — произвольные константы. Тогда   также является решением рассматриваемой системы.

Сформулируем теорему, которая позволит дать основное определение:

Теорема (о структуре общего решения). Пусть  , тогда: если  , где   — число переменных системы, то существует только тривиальное решение; если  , то существует   линейно независимых решений рассматриваемой системы:  , причём её общее решение имеет вид:  , где   — некоторые константы.

26

Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.

Квадратичная форма переменных   - функция

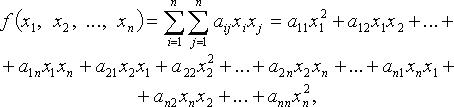
 - коэффициенты квадратичной формы. Без ограничения общности считают   тогда

     Если переменные   принимают действительные значения и   квадратичная форма называется действительной.

Матричная запись квадратичной формы 

     Матрица

называется матрицей квадратичной формы, ее ранг - рангом квадратичной формы. Квадратичная форма называется невырожденной, если 

     Главные миноры матрицы A называются главными минорами квадратичной формы.

     В пространстве   квадратичную форму можно записать в виде   где X - координатный столбец вектора 

     В пространстве   квадаратичную форму можно представить в виде   где f - линейный самосопряженный оператор, матрица которого в некотором ортонормированном базисе равна A.

27

 Метод ортогональных преобразований. Приведение квадратичной формы к каноническому виду. Ортогональное преобразование

        Линейное преобразование евклидова векторного пространства, сохраняющее неизменным длины или (что эквивалентно этому) скалярное произведение векторов. В ортогональном и нормированном базисе О. п. соответствует Ортогональная матрица. О. п. образуют группу (См. Группа) — т.н. группу вращений данного евклидова пространства вокруг начала координат. В трёхмерном пространстве О. п. сводится к повороту на некоторый угол вокруг некоторой оси, проходящей через начало координат О, если определитель соответствующей ортогональной матрицы равен +1. Если же этот определитель равен —1, то поворот дополняется зеркальным отражением относительно плоскости, проходящей через О и перпендикулярной оси поворота. В двумерном пространстве, т. е. в плоскости, О. п. определяет поворот на некоторый угол вокруг начала координат О или зеркальное отражение относительно некоторой прямой, проходящей через О. Используется О. п. при приведении к главным осям квадратичной формы 

28

Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.

Классификация действительных квадратичных форм       Положительно-определенные       Квадратичные формы, для которых  таких, что  Нормальный вид  Квадратичная форма является положительно-определенной тогда и только тогда, когда все ее главные миноры положительны  (критерий Сильвестра).      Отрицательно-определенные       Квадратичные формы, для которых  таких, что  Нормальный вид  Квадратичная форма является отрицательно-определенной тогда и только тогда, когда       Положительно-полуопределенные       Квадратичные формы, для которых  таких, что  Нормальный вид  r < n, r = rank A.      Отрицательно-полуопределенные       Квадратичные формы, для которых  таких, что  Нормальный вид  r < n, r = rank A.      Неопределенные       Квадратичные формы, которые принимают как положительные, так и отрицательные значения. Нормальный вид:  r = rank A.

Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой.

Пусть квадратичная форма имеет в каком-то базисе матрицу

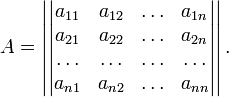
Тогда эта форма положительно определена, тогда и только тогда когда все её главные (угловые) миноры   положительны. Форма отрицательно определена, если и только если знаки   чередуются, причём  . Здесь главными минорами матрицы   называются определители вида

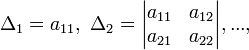
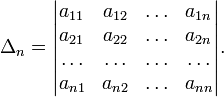
Для неотрицательно определённых матриц критерий действует только в одну сторону: если форма неотрицательно определена, то главные миноры неотрицательны. Обратное неверно. Например, матрица

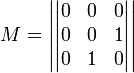
не является неотрицательно определённой — так как, например,   для  . В то же время все её главные миноры равны 0, то есть неотрицательны.

29

Вывод уравнения эллипса?????

30

Числовая последовательность — это последовательность элементов числового пространства.

Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе.