Каноническое уравнение прямой в пространстве

 

Пусть прямая проходит через точку M₁ (x₁, y₁, z₁) и параллельна вектору  (m ,n, l). Составим уравнение этой прямой.

 

                                   Z                                                                   

                                                                                                       

                                                                                                         

                                                                                                         

                                                                M                                      

                                                   M₁                                                 

                                                                                                         

                                                                    Y                                   

                                                                                                         

                           X                                                                            

                                                                                                         

 

Возьмем произвольную точку M (x, y, z) на этой прямой и найдем зависимость между x, y, z. Построим вектор

.

Векторы   и   коллинеарны.

 - каноническое уравнение прямой в пространстве.

Подвопрос

Взаимное расположение двух прямых и пространстве характеризуется следующими тремя возможностями.

1. Прямые лежат в одной плоскости и не имеют общих точек — параллельные прямые.

2. Прямые лежат и одной плоскости и имеют одну общую точку — прямые пересекаются.

3. В пространстве две прямые могут быть расположены еще так, что не лежат ни в одной плоскости. Такие прямые называются скрещивающимися (не пересекаются и не параллельны).

Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая пересекает эту плоскость и точке, которая не лежит на первой прямой, то эти прямые скрещиваются.

На рис. 26 прямая a лежит в плоскости , а прямая с пересекает   в точке N. Прямые a и с — скрещивающиеся.

Теорема. Через каждую из двух скрещивающихся прямых проходит только одна плоскость, параллельная другой прямой.

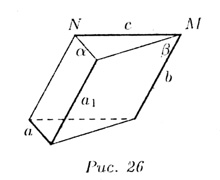
На рис. 26 прямые a и b скрещиваются. Черен прямую а проведена плоскость   || b (в плоскости   указана прямая a₁ || b).

Примеры скрещивающихся прямых: трамвайный рельс и троллейбусный провод по пересекающейся улице, нeпересекающиеся и непараллельные ребра пирамид или призм и пр. Все три случая можно видеть еще на примере прямых, по которым встречаются стены и потолок или стены и пол комнаты.

18

Матрицей размера mxn называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Вектор-строкой называют матрицу, состоящую из одной строки. Вектор-столбцом - из одного столбца. Матрица, у которой количество столбцов равно количеству строк, называется квадратной матрицей n-ого порядка. Элементы матрицы, у которых номер строки и номер столбца совпадает, называются диагональными и образуют главную диагональ матрицы. Если все недиагональные элементы матрицы равны нулю, то матрицу называют диагональной. Если у диагональной матрицы n-ого порядка на главной диагонали все элементы равны 1, то матрица называется единичной и обозначается Е. Матрица любого размера, все элементы которой равны 0, называется нуль-матрицей.

Матрицами называются массивы элементов, представленные в виде прямоугольных таблиц, для которых определены правила математических действий. Элементами матрицы могут являться числа, алгебраические символы или математические функции.

      Матричная алгебра имеет обширные применения в различных отраслях знания – в математике, физике, информатике, экономике. Например, матрицы используется для решения систем алгебраических и дифференциальных уравнений, нахождения значений физических величин в квантовой теории, шифрования сообщений в Интернете.

      Матрица обозначается одной из заглавных букв латинского алфавита, а набор ее элементов помещается в круглые скобки:

(1)

      Представленная формулой (1) матрица A имеет m строк и n столбцов и называется  m×n  матрицей (“эм на эн матрицей”) или матрицей размера  m×n. Строки матрицы нумеруются сверху вниз, а столбцы – слева направо.

19

Сложение и вычитание матриц - одно из простейших действий над ними, т.к. необходимо сложить или отнять соответствующие элементы двух матриц. Главное помнить, что складывать и вычитать можно только матрицыодинаковых размеров, т.е. тех, у которых одинаковое количество строк и одинаковое количество столбцов.

Умножение двух матриц возможно только при условии, что число столбцов первой матрицы должно равняться числу строк второй. Новая матрица, которая получится при умножении матриц, будет состоять из количества строк, равное количеству столбцов первой матрицы и количества столбцов, равное количеству строк второй матрицы.

Умножение на сколяр Умножение матрицы .При умножении матрицы  A  на число  λ  (слева или справа) каждый ее матричный элемент умножается на это число:

20

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

Существуют альтернативные методы нахождения обратной матрицы, например, метод Гаусса - Жордана. Суть метода заключается в том, что если с единичной матрицей Е провести элементарные преобразованиия, которыми невырожденная квадратная матрица А приводится к Е, то получится обратная матрица  .

21

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.

Ранг матрицы — Размерность образа   линейного оператора, которому соответствует матрица.

Обычно ранг матрицы   обозначается   ( ) или  . Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — для немецкого, французского и ряда других языков.

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.

22

Базисным минором матрицы называется любой её ненулевой минор максимального порядка. Для того чтобы минор был базисным, необходимо и достаточно, чтобы все окаймляющие его миноры (то есть содержащие его миноры на единицу большего порядка) были равны нулю. Система строк (столбцов) матрицы, связанных с базисным минором, является максимальной линейно независимой подсистемой системы всех строк (столбцов) матрицы.

Пример

Например, есть матрица:

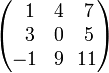
Минор   матрицы   ― определитель такой квадратной матрицы   порядка   (который называется также порядком этого минора), элементы которой стоят в матрице   на пересечении строк с номерами   и столбцов с номерами  .

Если номера отмеченных строк совпадают с номерами отмеченных столбцов, то минор называется главным, а если отмечены первые k строк и первые k столбцов ― угловым иливедущим главным.

23

Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений: