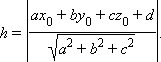Свойства смешанного произведения векторов

• Геометрический смысл смешанного произведения. Модуль смешанного произведения трех векторов равен объёму параллелепипеда, образованного этими векторами.

• Если смешанного произведения трех не нулевых векторов равно нулю, то эти векторами компланарные.

Смешанным произведением трех векторов   называется число

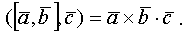
Модуль смешанного произведения трех векторов численно равен объему параллелепипеда, построенного на этих векторах.

П усть   правая тройка векторов (рис. 9). Действительно, объем параллелепипеда, построенного на векторах  , равен площади основания   на высоту . Здесь φ - угол между векторами  и 

Знак смешанного произведения совпадает со знаком cos φ, и поэтому смешанное произведение положительно, когда тройка векторов правая, и отрицательно, если тройка векторов левая.

9

Смешанное произведение трех векторов

Тройкой векторов называются три вектора, если указано, какой из них считается первым, какой вторым и какой третьим. Тройку векторов записывают в порядке нумерации; например, запись  ,  ,   означает, что вектор   считается первым,   - вторым,   - третьим.

Тройка некомпланарных векторов  ,  ,   называется правой, если составляющие ее векторы, будучи приведены к общему началу, располагаются в порядке нумерации аналогично тому, как расположены большой, указательный и средний пальцы правой руки. Если векторы  ,  ,   расположены аналогично тому, как расположены большой, указательный и средний пальцы левой руки, то тройка этих векторов называется левой.

Смешанным произведенем трех векторов  ,  ,   называется число, равное векторному произведению  , умноженному скалярно на вектор  , то есть  .

Имеет место тождество , ввиду чего для обозначения смешанного произведения   употребляется более простой символ  . Таким образом,

,  .

Смешанное произведение   равно объему параллелепипеда, построенного на векторах  ,  ,  , взятого со знаком плюс, если тройка   правая, и со знаком минус, если эта тройка левая. Если векторы  ,  ,   компланарны (и только в этом случае), смешанное произведение   равно нулю; иначе говоря, равенство

есть необходимое и достаточное условие компланарности векторов  ,  ,  .

Если векторы  ,  ,   заданы своими координатами:

,  ,  ,

то смешанное произведение   определяется формулой

.

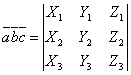Напомним, что система координатных осей предполагется правой (вместе с тем является правой и тройка векторов  ,  ,  ).

10

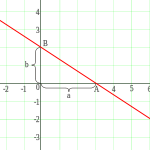
Уравнение прямой в отрезках это -- абсолютные величины чисел a и b равны длинам отрезков, которые отсекает прямая на координатных осях Ox и Oy, считая от начала координат.

Уравнение прямой линии, пересекающей ось   в точке   и образующей угол   с положительным направлением оси  :

Коэффициент   называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси 

Получение уравнения прямой в отрезках

[Править]Уравнение прямой в отрезках

Уравнение прямой линии, пересекающей ось   в точке   и ось   в точке  :

В этом виде невозможно представить прямую, проходящую через начало координат.

[Править]Нормальное уравнение прямой

где   — длина перпендикуляра, опущенного на прямую из начала координат, а   — угол (измеренный в положительном направлении) между положительным направлением оси   и направлением этого перпендикуляра. Если  , то прямая проходит через начало координат, а угол   задаёт угол наклона прямой.

Вывод нормального уравнения прямой  [показать]

Если прямая задана общим уравнением   то отрезки   и   отсекаемые ею на осях, угловой коэффициент   расстояние прямой от начала координат    и   выражаются через коэффициенты  ,   и   следующим образом:

Во избежание неопределённости знак перед радикалом выбирается так, чтобы соблюдалось условие   В этом случае   и   являются направляющими косинусами положительной нормали прямой — перпендикуляра, опущенного из начала координат на прямую. Если   то прямая проходит через начало координат и выбор положительного направления произволен.

11

Пусть даны точки A(x₁;y₁) и B(x₂;y₂). Уравнение прямой, проходящей через точки A(x₁;y₁) и B(x₂;y₂) имеет вид:

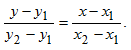 (8)

Если данные точки A и B лежат на прямой, параллельной оси O_x (у₂-у₁=0) или оси O_у (х₂-х₁=0), то уравнение прямой будет соответственно иметь вид у=у₁ или х=х₁

Пример 4. Составить уравнение прямой линии, проходящей через точки A(1;2) и B(-1;1).

Решение: Подставляя в уравнение (8) x₁=1, y₁=2, x₂=-1; y₂=1 получим:   откуда   или 2у-4=х-1, или окончательно х-2у+3=0

12

Угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых

1. Если прямые   и   заданы общими уравнениями

 

 и  ,

 

тогда угол между ними равен углу между их нормалями, то есть между векторами   и   

Следовательно,

.

 

Условия параллельности и перпендикулярности прямых тоже сводятся к условиям параллельности и перпендикулярности нормалей:

 – условие параллельности прямых   и  ;

 – условие перпендикулярности прямых   и  .

2. Если прямые   и   заданы каноническими уравнениями

 и  ,

где   и   направляющие векторы прямых   и  , то по аналогии с пунктом 1 получим:

,

 – условие параллельности прямых   и 

 – условие перпендикулярности прямых   и  .

3. Если прямые   и   заданы уравнениями с угловым коэффициентом

 и  ,

где    и  ,  и  углы наклона прямых к оси  , то для угла   между прямыми справедливо равенство:  .

Тогда

.

Итак,  острый угол между двумя прямыми определяется по формуле

.

 – условие параллельности двух прямых;

 (или  - условие перпендикулярности двух прямых

13

Общее уравнение плоскости в декартовой системе координат записывается следующим образом: 

ax + by + cz + d = 0.

Если известно, что плоскость проходит через точку с координатами (x₀, y₀, z₀), то ее уравнение можно привести к виду 

a (x – x0) + b (y – y0) + c (z – z0) = 0.

Уравнение 

называется уравнением плоскости в отрезках на осях.

Нормаль к плоскости имеет координаты 

Угол между двумя плоскостями легко вычисляется по формуле скалярного произведения. Если эти плоскости задаются уравнениями a₁x + b₁y + c₁z + d₁ = 0 иa₂x + b₂y + c₂z + d₂ = 0, то угол между плоскостями равняется 

Расстояние от точки (x₀; y₀; z₀) до плоскости, задаваемой уравнением ax + by + cz + d = 0, равно 

14

Уравнение плоскости в отрезках 

где a, b, c - величины отрезков, отсекаемых плоскостью на осях координат.

     Нормальное уравнение плоскости 

где   - углы, образуемые нормальным вектором плоскости с осями координат; p - расстояние от начала координат до плоскости.

     Приведение общего уравнения плоскости к нормальному виду:

Здесь 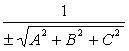  - нормирующий множитель плоскости, знак которого выбирается противоположным знаку D, если   произвольно, если D = 0.

15

Даны три точки

,

не лежащие на одной прямой. Требуется написать уравнение плоскости, проходящей через эти три точки. Из геометрии известно, что такая плоскость существует и единственная. Так как она проходит через точку  , то ее уравнение имеет вид

,      (9)

где  ,  ,   одновременно не равны нулю. Так как она проходит еще через точки  ,  , то должны выполняться условия:

                                          (10)

Составим однородную линейную систему уравнений относительно  неизвестных  ,  ,  :

                                           (11)

Здесь   есть произвольная точка, удовлетворяющая уравнению плоскости (9). В силу (9) и (10) системе (11) удовлетворяет нетривиальный вектор  , поэтому определитель этой системы равен нулю

.

Мы получили уравнение вида (9), т. е. уравнение плоскости, в чем легко убедиться, разложив полученный определитель по элементам первой строки. При этом эта плоскость проходит через точки  ,  ,  , что вытекает из свойств определителя. Наша задача решена.

Уравнение (12) можно еще написать и в следующем виде:

.                         (13)

Если из первой, третьей и четвертой строк определителя в (13) вычесть вторую строку, то он не изменится. Разлагая результат по элементам четвертого столбца, получим уравнение (12).

16

Возможны два случая взаимного расположения двух плоскостей в пространстве:

• Параллельны

• Пересекаться

Опр. Две плоскости в пространстве называются параллельными, если они не пересекаются, в  противном случаи они пересекаются.

Теорема1: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Доказательство:

Пусть  и - данные плоскости, а1 и а2 - прямые в плоскости , пересекающиеся в точке А, в1 и в2 - соответственно параллельные им прямые в

плоскости . Допустим, что плоскости  и  не параллельны, т.е. пересекаются по некоторой прямой с. По теореме прямые а1 и а2, как параллельные прямым в1и в2, параллельны плоскости , и поэтому они не

пересекают лежащую в этой плоскости прямую с. Таким образом, в плоскости  через точку А проходят две прямые (а1 и а2) , параллельные прямой с. Но это невозможно по аксиоме параллельных. Мы пришли к противоречию ЧТД.

Перпендикулярные плоскости: Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.

Теорема2: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Доказательство:

Пусть  - плоскость, в -перпендикулярная ей прямая,  - плоскость, проходящая через прямую в, с - прямая, по которой пересекаются плоскости  и . Докажем, что плоскости  и  перпендикулярны. Проведем в плоскости  через точку пересечения прямой в с плоскостью  прямую а,

перпендикулярную прямой с. Проведем через прямые а и в плоскость . Она перпендикулярна прямой с, т.к. прямая с перпендикулярна прямым а и в. Т. к. прямые а и в перпендикулярны, то плоскости  и  перпендикулярны. ч.т.д.

17