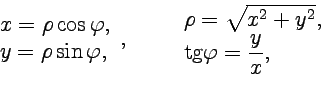1

Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:

1. Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда 

   a = c и b = d.

2. Суммой двух комплексных чисел a + ib и c + id называется комплексное число 

   a + c + i(b + d).

3. Произведением двух комплексных чисел a + ib и c + id называется комплексное число 

ac – bd + i(ad + bc).

Алгебраическая форма

Запись комплексного числа   в виде  ,  , называется алгебраической формой комплексного числа.

Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что  ):

2

Действия с комплексными числами, заданных в алгебраической форме

Свойство сложени: Сумма двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1+z2= a+bi + c+di = a+c +(b+d)i 

Пример:  5+3i + 3−i =8+2i 

Свойство вычитания: Разность двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1−z2= a+bi − c+di = a−c +(b−d)i 

Пример: .  5+3i − 3−i =2+4i 

Свойство умножения: Произведение двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1 z2= a+bi c+di = ac−bd +(ad+bc)i 

Пример:  3+2i 4−i =12−3i+8i−2i2=14+5i 

Свойство деления: Частное двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z2z1=c+dia+bi=c2+d2ac+bd+c2+d2bc−adi

Пример: . 1+i2+i= 1+i 1−i 2+i 1−i =1−i22−2i+i−i2=23−21i 

3

Комплексное число   изображается на плоскости точкой или, эквивалентно, вектором с координатами   (рис.1), и при таком способе задания  операции сложения будет соответствовать векторное сложение. Плоскость называется комплексной плоскостью, ось   - действительной осью и  - мнимой осью.

Рис.1.

В полярной системе координат на комплексной плоскости число   будет определяться парой действительных чисел   (рис.1). Из уравнений, связывающих декартовую и полярную системы координат, следует:

(8)

и   имеет смысл модуля , а   называется аргументом числа  ,  . С использованием (8) число   запишется как

(9)

и называется тригонометрической формой записи комлексного числа  . Отметим, что аргумент определен с точностью до целого кратного  , что записывается как

(10)

Выражение в скобках формулы (9) может быть преобразовано с помощью соотношения:

(11)

которое называется формулой Эйлера и позволяет получить еще один способ записи комплексных чисел

(12)

Выражение (12) называется показательной формой записи комплексного числа и является одной из наиболее часто встречающихся в комплексном анализе. Использование символа экспоненты в (11) указывает на то, что эта величина должна обладать и теми же свойствами. Доказательство последнего утверждения будет удобнее рассмотреть на примере.

     Пример 1-3. Доказать следующие свойства экспоненты с чисто мнимым показателем:

1.     2.      3. 

     Решение

1. Из формулы Эйлера (11) следует, что

2. Применяя формулу Эйлера два раза, получим

3. Поступая аналогично примеру 2 и учитывая правило деления комплексных чисел (7), получим

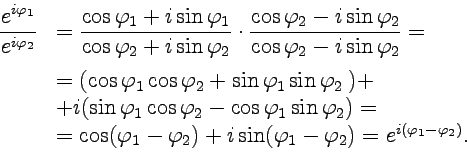
5

Возведение в степень комплексных чисел

        Операцию возведения в степень удобнее выполнять, когда комплексное число записано в тригонометрической или в показательной форме.

1. ,

2. .

Для возведения комплексного числа в степень нужно модуль возвысить в эту степень, а аргумент умножить на показатель степени.

Извлечение корня

Определение. Корнем n -ой степени из комплексного числа называется такое комплексное число, n -я степень которого равна подкоренному числу.

Из этого определения следует, что из равенства   следует равенство  .

         Из равенства комплексных чисел следует  , а аргументы отличаются на число, кратное   ;  . Отсюда  ,  . Здесь  есть арифметическое значение корня, а k  – любое целое число. Таким образом, получается формула .

В этой формуле число k может принимать всевозможные целые значения, но различных значений корня будет только n и они соответствуют значениям k  = 0, 1, 2, … , n  -  1.

        Докажем этот факт. Действительно, правые части в этой формуле различны тогда, когда аргументы   и   отличаются на величину, не кратную   , и будут одинаковыми, если указанные аргументы отличаются на величину, кратную   . Поэтому разность

не может быть кратна   .  Из этого результата и следует, что любым подряд взятым n целым числам k соответствуют n различных значений корня.

6

Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины вектора x на проекциювектора y на вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.

Обычно используется одно из следующих обозначений:

,

,

,