1.2. Аппроксимация переходной характеристики объекта по возмущающему каналу

Исследуемый объект по возмущающему каналу также является объектом с самовыравниванием (рис.5.). Поэтому аппроксимирующая передаточная функция примет форму оператора (1.1).

Рис. 5. Переходная характеристика по возмущающему каналу

Проведём касательную к экспериментальной переходной характеристике в точке перегиба с координатами (t_п; h(t_п)). Определим параметры передаточной функции:

К_об = h_уст = 0,28; _о = 3,5 с; Т_о = 7,9 с; h(t_п) = 0,07; t_п = 5,5 с

Аппроксимация переходной характеристики объекта по возмущающему каналу, как и в предыдущем случае, будет осуществляться с помощью 4,5,6 моделей.

1. Для получения четвертой модели воспользуемся выражением (1.2).

Параметры модели определяем по методу Лукаса[1]:

где, ;

Таким образом, получили четвертую математическую модель:

2. Воспользовавшись выражением (1.3) аналогично найдем пятую модель:

t₁=8,1с = 0 с

t₂= t₁ - = 8,1 – 0 = 8,1 c T_a2 = 0,64*t₂= 0,64*8,1 = 5,184 c

T_a1 =0,5 * T_a2 =0,5*5,184 = 2,592 c = =0 c

Подставляя полученные параметры в (1.3) получим:

Модель 5 считается наилучшей если h(0,5*t₂) ≥ 0,3*k_об (*)

где, h(0,5*t₂) = 0,03 0,3*k_об = 0,084

следовательно h(0,5*t₂) ≤ 0,3*k_об - условие не выполняется.

3. Так как (*) не выполняется, воспользуемся выражением (1.4) для получения 6 модели.

Аналогично по номограмме (рис.3.) находим Т^’_а1, Т^’_а2 по известным и .По известному значению находим значение , после чего определяем , и, следовательно:

Подставляем рассчитанные значения в формулу (1.4):

Далее с помощью ППП «MATLAB» на ЭВМ строим переходные процессы полученных функций (рис.6).

Вычислим погрешности аппроксимации полученных передаточных функций по интегральному критерию по формуле:

где:

- аппроксимирующая переходная характеристика;

- заданная переходная характеристика.

Выбираем передаточную функцию, имеющую наименьшую погрешность аппроксимации:

(1.6)

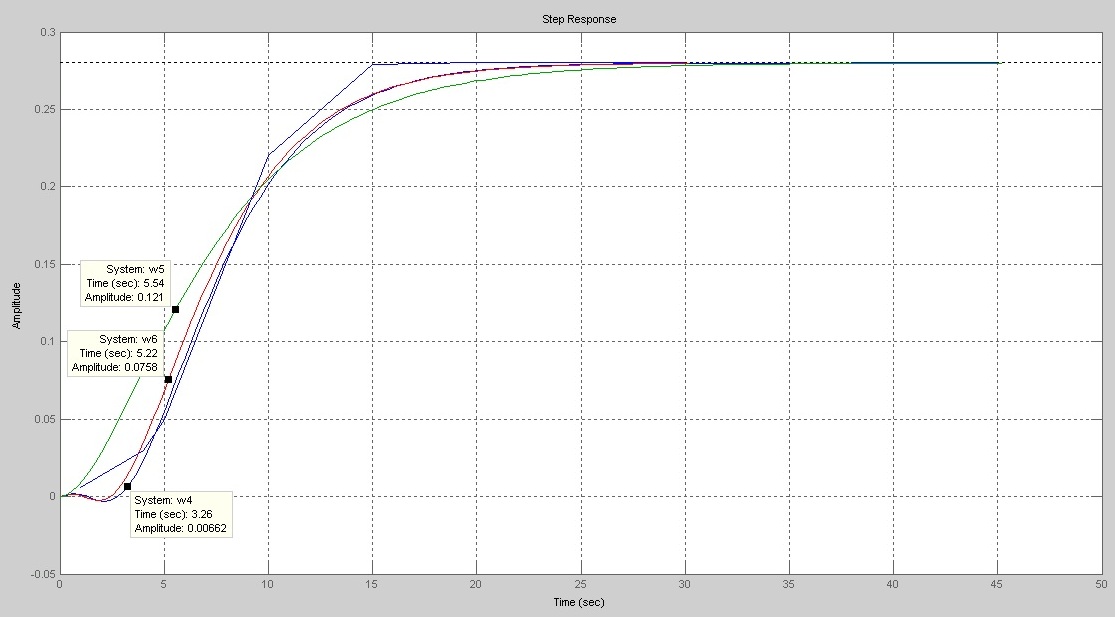
Рис. 6 Переходные характеристики моделей объекта управления по возмущающему каналу и заданная экспериментально переходная характеристика по возмущающему каналу.

1 -

2 -

3 -

4 - заданная экспериментально переходная характеристика по управляющему каналу

2. Выбор пи-алгоритма управления

В качестве показателя оптимальности АСР принимается минимум интеграла от квадрата ошибки системы при действии на объект наиболее тяжелого ступенчатого возмущения по регулирующему каналу (интегральный квадратичный критерий) с учетом добавочного ограничения на запас устойчивости системы, т.е.

. (2.1)

Такой критерий допускает значительное перерегулирование и увеличивает время регулирования, но он обеспечивает наименьшее максимальное динамическое отклонение регулируемой величины.

При практических расчётах запас устойчивости удобно характеризовать показателем колебательность системы М, значение которого в САУ, имеющих интеграл в алгоритме управления, совпадает с максимумом амплитудно-частотной характеристики системы:

(2.2)

где:

_р - резонансная частота, на которой А_з() имеет максимум.

Чтобы максимум не превышал некоторой заданной величины М, амплитудно-фазовая характеристика (АФХ) разомкнутой системы W_раз(j) не должна заходить внутрь «запретной» области ограниченной окружностью, центр u_o и радиус R_o которой определяется через М формулами (2.3) и (2.4), (рис.7):

(2.3)

. (2.4)

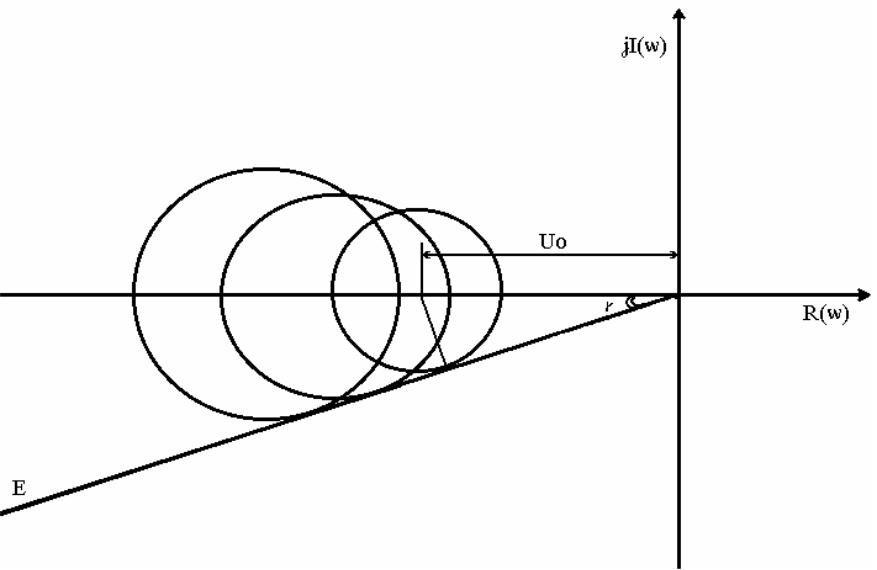
Рис.7. Определение центра и радиуса окружности, соответствующей заданному показателю колебательности М

Если же W_раз(j) касается указанной окружности, то это означает, что САУ находится на границе заданного запаса устойчивости.

На практике чаще всего принимают . При этом в САУ перерегулирование   40%, максимальное отклонение регулируемого параметра при внутренних возмущениях (возмущениях по регулирующему воздействию) не превышает 10%.