ЧАСТЬ ВТОРАЯ

ОСНОВЫ ТВЕРДОТЕЛЬНОЙ ЭЛЕКТРОНИКИ

9. Контактные явления

9.1. Эмиссия электронов.

Полная и термодинамическая работа выхода

Работа твердотельных приборов немыслима без использования различного вида контактов между различными телами. Это контакты между металлами, различающимися химическими свойствами (при­боры для измерения температуры — термопары), контакты между металлами и полупроводниками (омические контакты, диоды Шотт- ки), контакты между полупроводниками различного типа проводи­мости (полупроводниковые диоды, триоды, тиристоры и т. п.). Изу­чение особенностей контактов разных типов является принципиаль­но необходимой стадией при разработке приборов.

Контактирующие области приборов с физической точки зрения представляют собой различные по своим характеристикам электрон­ные (дырочные) коллективы, могущие обмениваться частицами в процессе установления равновесия между ними. Закономерности эмиссии (физики выхода электронов наружу) являются предметом рассмотрения в этом параграфе.

Явление выхода электронов из различных тел называют эмиссией электронов.

Если выход электронов обусловлен нагреванием тел, то эмиссию называют термоэлектронной.

Металлы содержат огромное количество электронов (до ) находящихся в тепловом движении и непрерывно подхо­дящих к поверхности.

Однако если металл не нагрет, выход электро­нов за его пределы практически равен нулю. Связано это с тем, что на электрон, стремящийся выйти из металла, действуют силы, препятст­вующие его выходу. Эти силы имеют двоякую природу.

Во-первых, это сила зеркального отображения: на электрон, находящийся на рас­стоянии от поверхности металла, со стороны металла действует та­кая сила, которая эквивалентна силе, действующей между двумя за­рядами противоположного знака, находящимися друг от друга на рас­стоянии (рис. 9.1):

Р и с. 9.1. Силы зеркального отражения

, (9.1)

где — диэлектрическая постоянная вакуума.

Полученное выражение для силы зеркального отображения спра­ведливо лишь для расстояний, существенно больших межатомных, когда можно пренебречь дискретностью поверхности и считать ее од­нородной.

На меньших расстояниях возвращающей электрон силой является сила двойного электрического слоя, образованного облаком электронов, вышедших из металла в вакуум, и положительно заря­женной приповерхностной областью металла (рис. 9.2).

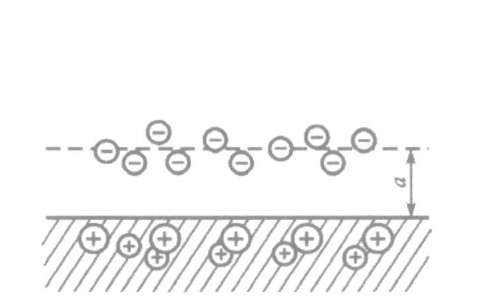
Рис. 9.2. Образование двойного электрического поля у поверхности металла

Действитель­но, даже при небольших часть электронов металла обладает доста­точно большой энергией и может выйти из металла (см. рис. 4.5).

Та­кой двойной электрический слой можно рассматривать как плоский конденсатор, расстояние между обкладками которого обозначим че­рез а. Напряженность поля внутри конденсатора считают постоян­ной. Эта модель была предложена В. Шоттки.

Силу, действующую на электрон со стороны двойного слоя, определяют по формуле

. (9.2)

Если предположить, что , при выходе за пределы двойного электрического слоя непрерывно переходит в силу зеркального изо­бражения , можно представить график возвращающих сил в виде, показанном на рис. 9.3.

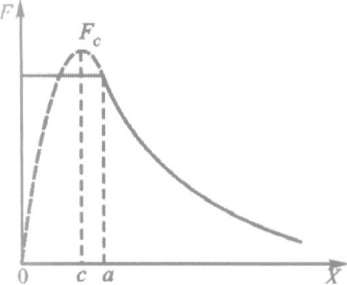
Р и с. 9.3. Зависимость возвращающей силы от

Работу, которую должен совершить электрон при выходе из ме­талла, определяют по формуле

. (9.3)

Полученное значение для величины характеризует глубину по­тенциальной ямы на границе металл—вакуум и называется полной ра­ботой выхода электрона (рис. 9.4). Пунктирная прямая OO на этом ри­сунке есть энергия вышедшего в вакуум электрона ( ).

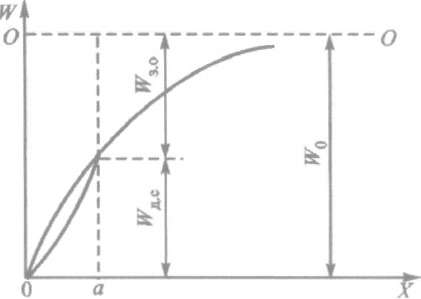
Р и с. 9.4. Энергетический барьер у поверхности металла ( - полная работа выхода)

Приближение плоского конденсатора оказывается недостаточно точным. Дело в том, что на свободный электрон в металле не действу­ет никакая сила, поэтому при эмиссии сила, возвращающая электрон, должна расти от нуля до некоторого максимального значения, переходя затем в силу зеркального отображения (пунктирная кривая на рис. 9.3).

И. Ленгмюр предложил описывать изменение этой силы в пределах двойного электрического слоя как

; (9.4)

при очевидных граничных условиях: , 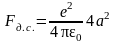. При этом полная работа выхода остается той же, что и у В. Шоттки.

Следует иметь в виду, что расстояние между обкладками кон­денсатора никак не определено. Можно лишь предположить, что оно должно быть равно нескольким межатомным расстояниям кристалла, чтобы выполнялось предположение об однородности поверхно­сти металла.

Поэтому количественные данные о величине полной ра­боты выхода можно получить лишь экспериментально, исследуя дифракцию электронов на кристаллической решетке.

В результате экспериментов было установлено, что для различных металлов значения лежат в пределах 3,5...18 эВ.

Поскольку в металлах подавляющее число электронов имеет энергию, близкую к энергии Ферми, то в уравнение, определяющее плотность тока термоэмиссии,

, (9.5)

входит величина 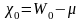, называемая термодинамической рабо­той выхода. Здесь 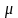— химический потенциал электронного газа в ме­талле, .

Ниже приведены значения , и для некото­рых металлов:

	, эВ	, эВ	, эВ
Li……………………………………	6,9	4,7	2,2
Na ………………………………….	5,0	3,1	1,9
Cu …………………………………..	11,1	7,04	4,06
Al …………………………………..	14,7	11,7	3,0

Уравнение, аналогичное (9.5), было получено и для плотности тока полупроводников:

. (9.6)

Величину 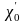называют эффективной работой выхода или просто работой выхода,

на энергетической шкале она представляет собой расстояние от уровня химического потенциала полупроводника до нулевого уровня. Иногда, так же как и в металлах, называют термо­динамической работой выхода.

Расстояние от дна зоны проводимости полупроводника до нуле­вого уровня называют в полупроводнике внешней работой выхода .

Подчеркнем важное отличие между металлами и полупроводниками в ходе термоэмиссии: если в металлах значение химического потен­циала является практически постоянным, то в полупроводнике уро­вень химического потенциала зависит от (см. рис. 4.9).