Матрица перехода

Ма́трицейперехо́да от базиса   к базису   является матрица, столбцы которой — координаты разложения векторов   вбазисе  .

Обозначается 

. Так как

.

.

.

.

Матрица перехода это

46. Преобразование координаты вектора при замене базиса.

. Пусть системы векторов e = {e₁, ..., e_n} и f = {f₁, ..., f_n} — два базиса n-мерного линейного пространства L_n.

Обозначим x_e = (x₁,x₂, ..., x_n) и x_f = (x'₁,x'₂, ..., x'_n) — координаты вектора x ∈ L_n соответственно в базисах e и f.

Справедливо следующее x_e= C_e→f·x_f :

Здесь C_e→f — матрица перехода от базиса e к базису f, это матрица, столбцами которой являются координаты базисных векторов f₁, ..., f_n  в базисе  e₁, ..., e_n:

f₁ = с₁₁· e₂ + с₂₁· e₁ + ... + с_n1· e_n, f₂ = с₁₂· e₁ + с₂₂· e₂ + ... + с_n2· e_n, ..., f_n = с_1n· e₂ + ... + с_nn· e_n.

Формулу преобразования координат вектора при изменении базиса принято записывать в виде

x_f= (C_e→f)^{− 1}·x_e

47. Понятие линейного подпространства. Подпространства решений однородной системы линейных алгебраических уравнений.

Подпространство

Алгебраическое определение: Линейное подпространство или векторное подпространство ― непустое подмножество K линейного пространства L такое, что K само является линейным пространством по отношению к определенным в L действиям сложения и умножения на скаляр. Множество всех подпространств обычно обозначают как Lat(L). Чтобы подмножество было подпространством, необходимо и достаточно, чтобы

• ;

• для всякого вектора  , вектор   также принадлежал K, при любом  ;

• для всяких векторов  , вектор   также принадлежал K.

Последние два утверждения эквивалентны следующему:

• для всяких векторов  , вектор   также принадлежал K для любых  .

В частности, пространство, состоящее из одного элемента {θ}, является подпространством любого пространства; любое пространство является само себе подпространством. Подпространства, не совпадающие с этими двумя, называют собственными или нетривиальными.

Свойства подпространств:

• Пересечение любого семейства подпространств — снова подпространство;

• Сумма конечного семейства подпространств — снова подпространство. Сумма подпространств   определяется как множество, содержащее всевозможные суммы элементов K_i:

.

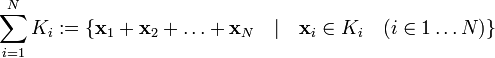В функциональном анализе в бесконечномерных пространствах особо выделяют замкнутые подпространства.

48. Линейные операторы (примеры)

Примеры линейных однородных операторов:

• оператор дифференцирования:  ;

• оператор интегрирования:  ;

• оператор умножения на определённую функцию  ;

• оператор интегрирования с заданным «весом» 

• оператор взятия значения функции f в конкретной точке x₀: L{f} = f(x₀)^[4];

• оператор умножения вектора на матрицу: b = Ax;

• оператор поворота вектора.

Примеры линейных неоднородных операторов:

• Любое аффинное преобразование;

• ;

• ;

• ;

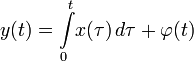где  ,  ,   — вполне определённые функции, а x(t) — преобразуемая оператором функция.

49. Матрица линейного оператора. Определение координат образа вектора линейного пространства при действии на него линейного оператора.

Матрица линейного оператора — матрица, выражающая линейный оператор в некотором базисе. Для того, чтобы ее получить, необходимо подействовать оператором на векторы базиса и координаты полученных векторов (образов базисных векторов) записать в столбцы матрицы.

Матрица оператора аналогична координатам вектора. При этом действие оператора на вектор равносильно умножению матрицы на столбец координат этого вектора в том же базисе.

Выберем базис  . Пусть   — произвольный вектор. Тогда его можно разложить по этому базису:

,

где x^k — координаты вектора   в выбранном базисе.

Здесь и далее предполагается суммирование по немым индексам.

Пусть   — произвольный линейный оператор. Подействуем им на обе стороны предыдущего равенства, получим

.

Вектора   также разложим в выбранном базисе, получим

,

где   — j-я координата k-го вектора из  .

Подставим разложение в предыдущую формулу, получим

.

Выражение  , заключённое в скобки, есть ни что иное, как формула умножения матрицы на столбец, и, таким образом, матрица   при умножении на столбец x^k даёт в результате координаты вектора  , возникшего от действия оператора   на вектор  , что и требовалось получить.

 Комментарий: Если в полученной матрице поменять местами пару столбцов или строк, то мы, вообще говоря, получим уже другую матрицу, соответствующую тому же набору базисных элементов  . Иными словами, порядок базисных элементов предполагается жёстко упорядоченным.

50. Связь между матрицами линейного операторы в разных базисах.

Связь между матрицами одного и того же линейного оператора в разных базисах 

     Если в базисе   линейный оператор   имеет матрицу A, в базисе   - матрицу B, а S - матрица перехода от первого базиса ко второму, то

51. Собственные числа и собственные векторы линейного операторы (включая способ их нахождения)

Собственные векторы и собственные значения линейного оператора 

    Ненулевой вектор 

называется собственным вектором линейного оператора  , если   (  для комплексного  ), такое, что   Число   называется собственным числом (собственным значением) оператора f, соответствующим этому собственному вектору.

    Если в некотором базисе оператор f имеет матрицу А и в том же базисе вектор   имеет координатный столбец X, то   или 

    Собственные числа   линейного оператора   - корни характеристического уравнения  , где   - матрица оператора f,   - символ Кронекера.

   Для каждого собственного значения   соответствующие собственные векторы могут быть найдены из матричного уравнения   или соответствующей ему системы линейных уравнений

    Линейный оператор называется оператором простой структуры, если существует базис, состоящий из собственных векторов этого оператора. Матрица линейного оператора в этом базисе имеет вид

где   - соответствующие собственные значения.

52. Диагональная форма матрицы. Каноническое разложения матрицы линейного оператора.

Диагональная матрица имеет вид:

Такая матрица является одновременно и верхетреугольной и нижнетреугольной.