1. Матрицы. Действия с матрицами и их свойства. Транспонирование матрицы

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы.

Матрицы допускают следующие алгебраические операции:

сложение матриц, имеющих один и тот же размер;

умножение матриц подходящего размера (количество строк одной матрицы должно совпадать с количеством столбцов другой);

умножение матрицы на элемент основного кольца или поля (т. н. скаляр).

Транспонированная матрица — матрица A^T, полученная из исходной матрицы A заменой строк на столбцы.

Формально, транспонированная матрица для матрицы A размеров   — матрица A^T размеров  , определённая как A^T[i, j] = A[j, i].

Свойства транспонированных матриц

Дважды транспонированная матрица А равна исходной матрице А.

Транспонированная сумма матриц равна сумме транспонированных матриц. Транспонированное произведение матриц равно произведению транспонированных матриц

При транспонировании можно выносить скаляр

. Определитель транспонированной матрицы равен определителю исходной матрицы.

2. Определители и их свойства

.Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равны)

Меняя столбцы или строки местами, величина определителя не меняется.

Перестановив строки или столбцы местами определитель умножается на -1.

Если есть нулевая строка(столбец) то определитель равен нулю

Раевн нулю если есть пропорциональные или равные строки

Если к элементам одной строки(столбца) прибавить элементы другого столбца(строки)

То величина определителя не изменится.

3. Определение минора и алгебраического дополнения данного элемента матрицы. Две теоремы связанные с понятием алгебраического дополнения

Минором элемента   определителя  – го порядка называют определитель  – го порядка, который получается из данного определителя вычеркиванием  - й строки и  – го столбца, на пересечении которых стоит элемент  .

 Алгебраическим дополнением элемента   определителя  – го порядка называют его минор, взятый со знаком плюс, если   – четное число и со знаком минус в противном случае.

Обозначение:  .

Теорема (о разложении определителя по заданной строке или столбцу). Определитель равен сумме произведений элементов какой–либо его строки (или столбца) на их алгебраические дополнения.

4. Понятие обратной матрицы теорема о существовании обратной матрицы

.Понятие обратной матрицы вводится только для квадратных матриц.

Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая

 A^-1 и удовлетворяющая условию  . (Это определение вводится по аналогии с умножением чисел)

Справедлива следующая теорема:

Теорема. Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.

5. Решение матричных уравнений с помощью обратной матрицы. Решение систем линейных алгебраических уравнений с невырожденной матрицей. Метод Крамера.

5.Матричные уравнения могут иметь вид:

АХ = В, ХА = В, АХВ = С,

где А,В,С — задаваемые матрицы, Х- искомая матрица.

Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.

Например, чтобы найти матрицу Х из уравнения АХ = В, необходимо умножить это уравнение на А^-1 слева и справа.

Тогда: 

Описание метода(краммер)

Для системы n линейных уравнений с n неизвестными (над произвольным полем)

с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде

(i-ый столбец матрицы системы заменяется столбцом свободных членов).

6. Метод Гаусса. Теорема о наличии ненулевого решения однородной системы линейных алгебраических уравнений с прямоугольной матрицей А(mxn) при n>m.

Ме́тодГа́усса^[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные

Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

Если ранг меньше числа строк то система имеет свободные переменные и бесконечное число решений. Если арнг равен строкам то есть одно решение.

Когда n>m то есть число неизвестных больше то решений очень много.

В процессе исключений метода гаусса не может возникнуть более m не нулевых ведущих элементов или не нулевых ведущих строк то число свободных переменных не может быть меньше чем n-m.

Каждая однородная система АХ=0 имеющая больше неизвестных чем уравнений имеет хотя б одно не нулевое решение

7. Понятие линейной зависимости арифметических векторов (примеры)

Система векторов e₁,e₂, ..., e_k линейного пространства L называется линейно независимой системой, если равенство С₁·e₁+С₂·e₂+ ...+С_k· e_k = 0 возможно только когда все коэффициенты С₁, С₂, ..., С_k равны нулю.

Здесь 0 — нулевой вектор линейного пространства L, С₁, С₂, ..., С_k — числовые коэффициенты.

  Если система векторов e₁,e₂, ..., e_k линейного пространства L не является линейно независимой системой, то она называется линейно зависимой системой векторов.

пример

Система векторов ·i, j линейного пространства R₂ геометрических радиусов векторов плоскости линейно независима. Действительно.

i = (1, 0),  j = (0, 1),   С₁·i + С₂· j = (С₁, С₂), а из (С₁, С₂) = 0 следует, что  С₁ = 0 и С₁ = 0, т.е. система векторов i,j из R₂ линейно независима.

8. Понятие базиса системы арифметических векторов (примеры) Второе определение базиса систем векторов

базисная система векторов v1 v2…. vk с n компонентами. Базисом этой системы векторов называется такое подмножество w1 w2 ….wr линейно-независимых, что любой v1 v2 …vk выражается в виде линейной комбинации векторов w1 w2 ….wr.

Ба́зис (др.-греч. βασιζ, основа) — множество таких векторов в векторном пространстве, что любой другой вектор пространства может быть единственным образом представлен в виде линейной комбинации базисных векторов.

9. Понятие ранга матрицы. Теорема о ранге ступенчатой матрицы.

Рангом системы векторов v1 v2…. vk называется число базисных векторов данной системы.

Ранг системы столбцов матрицы равен рангу системы строк матрицы

 Если матрица A не нулевая, т.е. существует хотя бы один a_ij элемент матрицы A, отличный от нуля, тогда всегда можно указать натуральное число r такое, что

у матрицы A имеется минор r-го порядка, для которого Δ_r 0;

всякий минор матрицы A порядка r+1 и выше равен нулю, тогда число r, обладающее указанными свойствами называется рангом матрицы A и обозначается r = RgA.

ранг любой прямоугольной матрицы не должен быть больше, чем минимальный размер матрицы. Если матрица квадратная, то ранг не может быть больше, чем размер матрицы. Математически это можно выразить так r min(m,n).

если все элементы матрицы A равны нулю, т. е. a_ij=0, то ранг этой матрицы тоже будет равен нулю r = RgA = 0.

Ранг ступенчатой матрицы А равен числу её не нулевых строк или столбцов содержащих ведущие элементы.

10. Теорема о равенстве ранге произвольной матрицы А и эквивалентной ей ступенчатой матрицы (поясните на примере)

11. Теорема о существование ненулевого решения однородной системы линейных алгебраических уравнений с прямоугольной матрицей. Фундаментальная система решений.

Однородные системы

Однородной системой линейных уравнений называется система вида:

Нулевое решение   системы (1) называется тривиальным решением.

В матричной форме АХ=0

Однородная система всегда совместна тк существует тривиальное решение х1=х2=хn=0

Система не определена когда ранг матрицы меньше числа неизвестных

Теорема (о структуре общего решения). Пусть  , тогда:

• если  , где   — число переменных системы, то существует только тривиальное решение;

• если  , то существует   линейно независимых решений рассматриваемой системы:  , причём её общее решение имеет вид:  , где   — некоторые константы.

Теорема (о ФСР). Пусть ранг основной матрицы  , где   — число переменных системы (1), тогда:

• ФСР (1) существует:  ;

• она состоит из   векторов;

• общее решение системы имеет вид  .

Замечание: Если  , то ФСР не существует.

Пример

Решим систему

Перепишем её в матричном виде:

Путём элементарных преобразований над строками приведём её основную матрицу к ступенчатому виду:

Таким образом ранг системы (ранг её основной матрицы) равен двум. Это значит, что существует   линейно независимых решения системы.

Перепишем полученную систему в виде уравнений:

Возьмём   и   в качестве главных переменных. Тогда:

Подставим по очереди единицы в качестве одной из свободных переменных:   и  .

Тогда общее решение рассматриваемой системы может быть записано так:

,

а вектора   составляют фундаментальную систему решений.

12. Структура решения неоднородной системы линейных алгебраических уравнений.

Неоднородной системой линейных уравнений называется система вида:

 — её расширенная матрица.

Теорема (об общем решении неоднородных систем). Пусть   (т.е. система (2) совместна), тогда:

• если  , где   — число переменных системы (2), то решение (2) существует и оно единственно;

• если  , то общее решение системы (2) имеет вид  , где   — общее решение системы (1), называемое общим однородным решением,   — частное решение системы (2), называемое частным неоднородным решением.

Пример

Решим систему

Преобразуем её к

Тогда переменные   и   обязательно будут главными, возьмём также   в качестве главной.

Заметим, что   является частным решением.

Составим однородную систему:

Тогда, подставив единицу в качестве свободной переменной  , получим ФСР однородной системы:

Общее решение системы может быть записано так:

13. Теорема о связи ранга квадратной матрицы и ее определителя. Решение однородной и неоднородной систем уравнений с квадратной матрицей.

Пусть   . Определитель матрицы   равен нулю, так как третья строка равна сумме первых двух. Минор второго порядка, расположенный в первых двух строках и первых двух столбцах, равен   . Следовательно, ранг матрицы равен двум, и рассмотренный минор является базисным.

14. Понятие геометрического вектора. Линейные операции над векторами.

Понятие вектор в геометрии отлично от определяемого в алгебре.

• Связанный вектор или направленный отрезок — упорядоченная пара точек евклидова пространства.

При этом два направленных отрезка считаются эквивалентными, если они:

1. коллинеарны

2. равны по длине

3. сонаправлены

Суммой векторов является вектор - 

Произведение -  , при этом   коллинеарен  .

Вектор   сонаправлен с вектором  (  ­­ ), если a > 0.

Вектор   противоположно направлен с вектором  ( ­¯ ), если a < 0.

15. Разложение вектора по трем некомпланарным векторам.

Если дана упорядоченная тройка векторов   некомпланарных векторов, то для любого вектора  существует единственная упорядоченная тройка чисел  , удовлетворяющая равенству .

16. Проекция вектора на некоторые направление. Теоремы о проекциях.

проекцией вектора на ось называется произведение модуля вектора на косинус угла,образованного вектором и положительным направлением оси.

     

17. Координаты вектора. Направляющие косинусы.

.Координа́тыве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.

где   — координаты вектора.

• Равные векторы в единой системе координат имеют равные координаты

• Координаты коллинеарных векторов пропорциональны:

Подразумевается, что координаты вектора b не равны нулю.

• Квадрат длины вектора равен сумме квадратов его координат:

• При умножении вектора на действительное число каждая его координата умножается на это число:

• При сложении векторов соответствующие координаты векторов складываются:

• Скалярное произведение двух векторов равно сумме произведений их соответствующих координат:

• Векторное произведение двух векторов можно вычислить с помощью определителя матрицы

где

• Аналогично, смешанное произведение трех векторов можно найти через определитель

Направляющие косинусы вектора (в пространстве) – это косинусы углов, которые вектор образует с положительными полуосями координат. Направляющие косинусы однозначно задают направление вектора. Если вектор имеет длину 1, то его направляющие косинусы равны его координатам. В общем случае для вектора с координатами (a; b; c) направляющие косинусы равны:

где a, b, g – углы, составляемые вектором с осями x, y, z соответственно.

18. Понятие радиус-вектора данной точки пространства. Расстояние между двумя точками в пространстве.

Ра́диус-ве́ктор (обычно обозначается   или просто   ) — вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Теорема. Пусть   и  . Тогда

      .

19. Скалярное произведение векторов и его свойства.

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла междуними.

Обозначается ab,а* b(или( а, b)).Итак, по определению,

  

Формуле   (6.1)   можно   придать   иной   вид.   Так   как | a| cos=пр _ba, (см. рис.14), a |b| cos = пр_ab, то получаем:

      

 т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

 1. Скалярное произведение обладает переместительным свойством: ab=ba

  

20

Если векторы   и   заданы своими координатами:

,  ,

то их скалярное произведение может быть вычислено по формуле

20. Формула для вычисления скалярного произведения векторов.

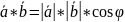
если

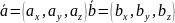
21. Векторное произведения и его свойства.

Векторное произведение и его св-ва

Векторным произведением неколлинеарных векторов 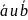называется вектор , определяемый условиями:

1. 

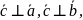
2. длина равно площади параллелограмма, построенного на векторах как на сторонах, т.е. :

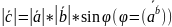
3. образующие правую тройку

пиздец изображениеце

Обозначение: 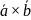или

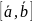
Свойства:

1. Антикоммутативность

2. Сочетательность (ассоциативностиь) по отношению к скалярному множетилю:

3. Распределительность (дистрибутивность):

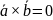4. , если

Если векторы заданы своими координатами:

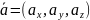, то

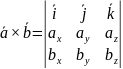или

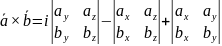
где S – площадь параллелограмма

22. Формула для вычисления векторного произведения векторов.

или

или

23. Смешанное произведение и его геометрический смысл

Смешанным произведением 3-х векторов называется число, равное скалярному произведению вектора на вектор

Обозначение: = (

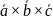Геометрический смысл:

Смешанным произведением интерпретируется как число, равное объему параллелограмма, построенного на векторах как на ребрах

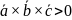, если образует правую тройку

, если образует левую тройку

24. Формула для вычисления смешанного произведения векторов. Условие компланарности трех векторов. Правая и левая тройка векторов.

Если заданы своими координатами , , то

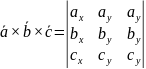–ф-ла для вычисления смешанного произведения векторов

Условие компланарности 3-х векторов:

3 ненулевых векторов компланарны тогда и только тогда, когда один из них является линейной комбинацией других, например

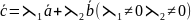
Правая и левая тройка векторов:

3 некомпланарных векторов , взятого в указанном порядке, образуют правую тройку (левую) тройку, если с конца вектора кратчайший поворот от первого вектора ко 2-му вектору виден совершающимся противчасовой стрелки (по часовой стрелки)ХУЙНЯ КАКАЯТО

25. Кривые второго порядка

Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

в котором по крайней мере один из коэффициентовa11, a 12, a22 отличен от нуля.

Классификация кривых второго порядка

Невырожденные кривые

Кривая второго порядка называется невырожденной, если Могут возникать следующие варианты:

• Невырожденная кривая второго порядка называется центральной, если

  • эллипс — при условии D> 0 и ΔI< 0;

    • частный случай эллипса — окружность — при условии I² = 4D или a₁₁ = a₂₂,a₁₂ = 0;

  • мнимый эллипс (ни одной вещественной точки) — при условии ΔI> 0;

  • гипербола — при условии D< 0;

• Невырожденная кривая второго порядка называется нецентральной, если ΔI = 0

  • парабола — при условии D = 0.

Вырожденные кривые

Кривая второго порядка называется вырожденной, если Δ = 0. Могут возникать следующие варианты:

• вещественная точка на пересечении двух мнимых прямых (вырожденный эллипс) — при условии D> 0;

• пара вещественных пересекающихся прямых (вырожденная гипербола) — при условии D< 0;

• вырожденная парабола — при условии D = 0:

  • пара вещественныхпараллельных прямых — при условии B< 0;

  • одна вещественная прямая (две слившиеся параллельные прямые) — при условии B = 0;

  • пара мнимыхпараллельных прямых (ни одной вещественной точки) — при условии B> 0.

Диаметры и центр кривой второго порядка

Диаметром кривой второго порядка называется геометрическое место середин параллельных хорд этой кривой. Полученный таким образом диаметр называется сопряжённым этим хордам или их направлению. Диаметр, сопряжённый хордам, образующих угол θ с положительным направлением оси Ox, определяется уравнением:

Если выполняется условие то все диаметры кривой пересекаются в одной точке — центре, а сама кривая называется центральной. В противном случае (D = 0) все диаметры кривой либо параллельны, либо совпадают.

Координаты центра определяются системой уравнений:

Решая эту систему относительно x₀ и y₀, получим:

Если кривая центральная, то перенос начала координат в её центр приводит уравнение к виду

где  — координаты относительно новой системы.

Главные оси и вершины кривой второго порядка

Главной осью кривой второго порядка называется её диаметр, перпендикулярный к сопряжённым к ним хордам. Этот диаметр является осью симметрии кривой. Каждая центральная кривая либо имеет две взаимно перпендикулярные оси, либо все диаметры являются главными осями. В последнем случае кривая является окружностью. Нецентральные кривые имеют лишь одну главную ось. Точки пересечения главной оси с самой кривой называются её вершинами.

Направляющие косинусы нормалей к главным осям удовлетворяют уравнениям

где λ — отличный от нуля корень характеристического уравнения. Направления главных осей и сопряжённых им хорд называются главными направлениями кривой. Угол между положительным направлением оси Ox и каждым из двух главных направлений определяется формулой

Из всех видов кривых второго порядка только окружность имеет неопределённые главные направления.

Уравнения

Общее уравнение в матричном виде

Общее уравнение кривой можно записать в матричном виде

Канонический вид

Вводом новой системы координат можно привести уравнения кривых второго порядка к стандартному каноническому виду (см. таблицу). Параметры канонических уравнений весьма просто выражаются через инварианты и корни характеристического уравнения (см. выше раздел «Характеристическая квадратичная форма и характеристическое уравнение»).

Вид кривой	Каноническое уравнение	Инварианты
Невырожденные кривые ( )
Эллипс
Гипербола
Парабола
Вырожденные кривые (Δ = 0)
Точка
Две пересекающиеся прямые
Две параллельные прямые
Одна прямая	x2 = 0

Для центральной кривой в каноническом виде её центр находится в начале координат.

Через эксцентриситет

Каноническое уравнение любой невырожденной кривой второго порядка при помощи подходящего преобразования начала координат может быть приведено к виду

В этом случае кривая проходит через начало новой системы координат, а ось Ox является осью симметрии кривой. Данное уравнение выражает тот факт, что невырожденная кривая второго порядка является геометрическим местом точек, отношение расстояний которых (эксцентриситет) от данной точки (фокуса) и от данной прямой (директрисы) постоянно. Кроме того, при кривая является окружностью, при  — эллипсом, при  — параболой, при  — гиперболой.

Уравнение директрисы кривой выражается уравнением а координаты фокуса Директриса перпендикулярна оси симметрии, проходящей через фокус и вершину кривой (фокальная ось). Расстояние между фокусом и директрисой равно

Если кривая второго порядка центральная (эллипс или гипербола), то прямая

является осью симметрии и, следовательно, кривая имеет два фокуса и две директрисы.

Параметр p называется фокальным параметром и равен половине длины хорды, проходящей через фокус и перпендикулярной к фокальной оси (фокальная хорда).

Полярные координаты

Если взять в качестве полюса полярной системы координат фокус невырожденной кривой второго порядка, а в качестве полярной оси — её ось симметрии, то в полярных координатах ρ, φ уравнение кривой будет иметь вид

Кривая, заданная своими пятью точками

Кривая второго порядка вполне определяется пятью своими точками, если никакие четыре из них не лежат на одной прямой. Уравнение кривой, проходящей через точки и

Кривая, заданная пятью точками вырождается в том и только в том случае, когда три из заданных точек лежат на одной прямой.

Касательные и нормали

Уравнение касательной к кривой второго порядка f(x,y) в её точке имеет вид:

Уравнение нормали к кривой второго порядка в точке имеет вид

Полюсы и поляры

Уравнение

помимо касательной опряделяет прямую, называемую полярой точки относительно кривой второго порядка, независимо от того, лежит ли эта точка на кривой или нет. При этом точка называется полюсом этой прямой. Поляра точки кривой есть её касательная в этой точке.

Теоремы о полюсах и полярах:

1. Если прямая, проведённая через полюс P, пересекает поляру в точке Q, а кривую второго порядка — в точках R₁ и R₂, то точки P и Qгармонически разделяют отрезок R₁R₂, т. е. выполняется условие

2. Если точка лежит на некоторой прямой, то её поляра проходит через полюс этой прямой. Если прямая проходит через некоторую точку, то её полюс лежит на поляре этой точки.

3. Диаметр кривой второго порядка есть поляра бесконечно удалённой точки, через которую проходят сопряжённые ему хорды, а центр кривой есть полюс бесконечно удалённой прямой.

4. Фокус кривой есть центр пучка, обладающего тем свойством, что полюс любой его прямой принадлежит перпендикулярной к ней прямой пучка. Директрисса есть поляра фокуса.

Из этих утверждений, в частности, следует, что:

1. если через точку можно провести две касательные к кривой, то то поляра этой точки проходит через точки касания;

2. касательные к кривой в концах диаметра параллельны сопряжённым ему хордам;

3. точка пересечения касательных к кривой в концах любой её хорды, проходящей через фокус, лежит на директриссе;

4. каждая хорда, проходящая через фокус, перпендикулярна к прямой, проведённой через её фокус и точку пересечения касательных в концах хорды.

26. Общее уравнение плоскости