Понятие информации и ее виды; подходы к оценке количества информации. Аналоговая и дискретная форма представления информации. Единицы дискретной информации.
Информация- это некоторая последовательность символических обозначений (букв, цифр, закодированных графических образов и звуков и т. п.), несущую смысловую нагрузку и представленную в понятном компьютеру виде. Каждый новый символ в такой последовательности символов увеличивает информационный объем сообщения.
Количество
информации
- это мера уменьшения неопределенности.
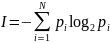, где
-вер-ть
отдельных событий, N-кол-во
возможных событий. БИТ- это наименьшая
единица измерения информации.
Аналоговая – физическая величина принримает бесконечное множество значений, ее значения изменяются непрерывно.
Дискретная – физическая величина принимает конечное множество значений и изменяется скачкообразно. Пример 0 и 1.
Понятие алгоритма. Операция. Программа. Команда. Укрупненная структура и принцип функционирования эвм.
К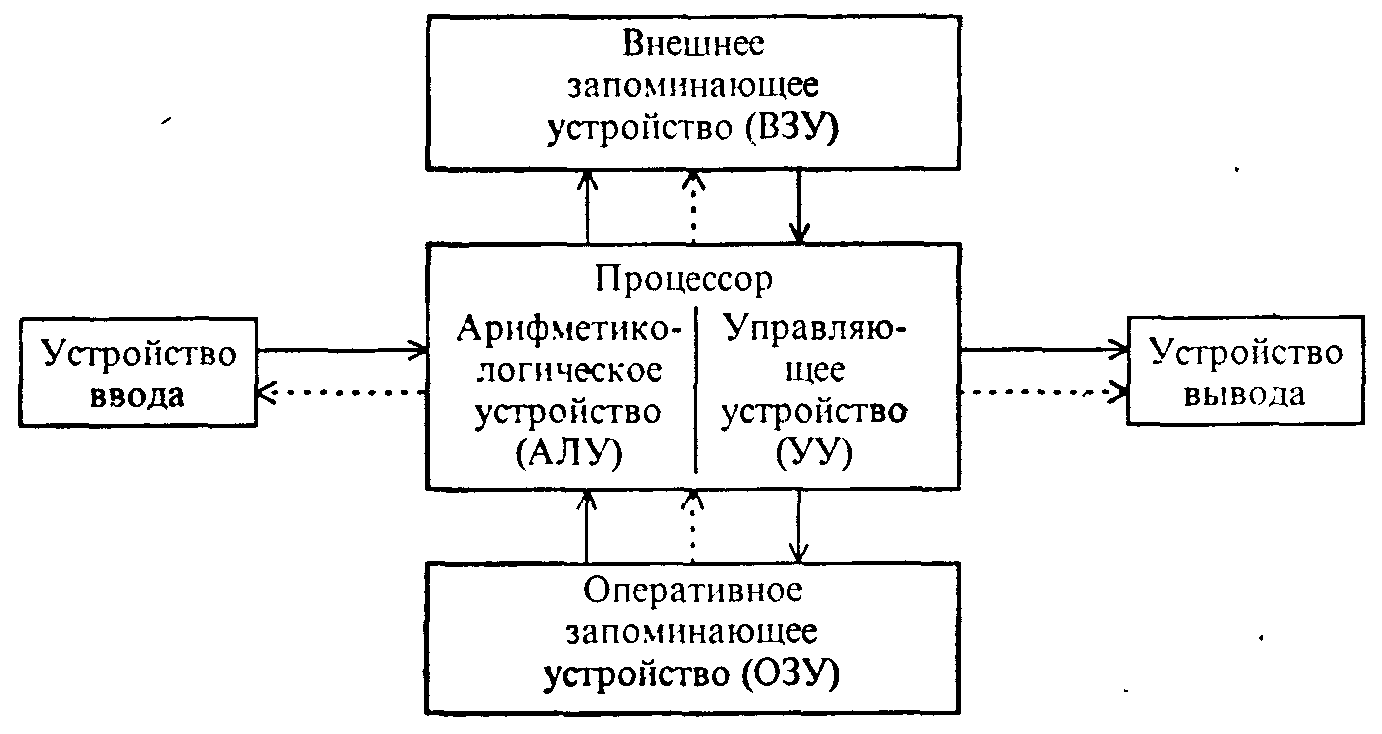
оманда-
элементарное
действие, операция, выполняемые
вычислительным устройством.
Способы представления дискретной информации. Позиционные и непозиционные системы счисления.
В позиционной – значение каждой цифры или символа зависит от положения(разряда).
Целое число без знака x в b-ричной системе счисления представляется в виде конечной линейной комбинации степеней числа b.
Пример: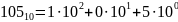
В непозиционной – каждая цифра не зависит от положения. Система может накладывать определенные ограничения на порядок цифр (расположение по возрастанию или убыванию).
Пример: римская система, в которой в качестве цифр используются латинские буквы.
Системы счисления, используемые в эвм - двоичная, восьмиричная, шестнадцатиричная и двоично-десятичные системы счисления.
Двоичная система счисления — позиционная система счисления с основанием 2. В этой системе счисления числа записываются с помощью двух символов (0 и 1).
Восьмеричная система счисления — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.
Шестнадцатеричная система счисления- позиционная система счисления по целочисленному основанию 16. Используются десятичные цифры от 0 до 9 и латинские буквы от A до F.
Двоично десятичная система- форма записи целых чисел, когда каждый десятичный разряд числа записывается в виде его четырёхбитного двоичного кода. Пример: число 819256 имеет 6 цифр 8 1 9 2 5 6, следовательно в двоично десятичной системе счисления это будет следующее число: 1000 0001 1001 0010 0101 0110
Перевод чисел из одной позиционной системы счисления в другую. Диапазон представления чисел со знаком и без знака. Точность представления числа.
Перевод чисел -
Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики
Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики
Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики
Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой
Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой
Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.
Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.
При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Диапазон представления
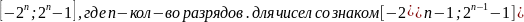
Точность представления числа – кол-во разрядов регистра определяет точность представления чисел.