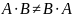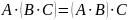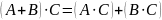Б начало лок – схемы простой итерации.

X₀, q, ε

X:=x₀

Y:=f(x₀)

∆=q/(1-q)*abs(y-x)

∆ >ε

- +

‘корень=’,y,’погрешность=',∆

конец

X:=x₀

Y:=f(x₀)

∆=q/(1-q)*abs(y-x)

Билет №14 Программная реализация метода простой итерации

ProgramP4;

functionf (z:real):real;

begin

f:=sin(sgr(z));

end;

varх0, q, e, x, y, d; real;

begin

writeln (‘введитех0, q, e');

readln (х0, q, e);

х:=х0;

у:=f(x0);

d:=q/(1-q)*abc(y-x);

while de do

begin

x:=y;

y:=f(x);

d:=q/(1-q)*abc(y-x);

end;

writeln (‘корень=’,y,’погрешность=’,d);

end.

Билет №15 Матрицы и определители

Матрицей называется множество чисел образующих прямоугольную таблицу, которая содержит m - строк и n – столбцов.

Для записи используют обозначения:

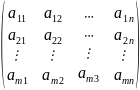
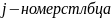
Сокращенно, матрицу типа 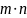записывают A или

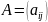
Если число строк матрицы не равно числу столбцов 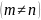, то матрица называется прямоугольной.

Если число строк матрицы равно числу столбцов 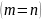, то матрица называется квадратной.

Число строк или столбцов квадратной матрицы называется ее порядком.

Пример:

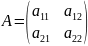– квадратная матрица второго порядка.

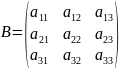– квадратная матрица третьего порядка

Диагональ квадратной матрицы.

Диагональ, содержащую элементы называют главной, а диагональ, содержащую элементы называют побочной или вспомогательной.

Среди квадратных матриц выделяют так называемые диагональные:

Все элементы нули, и только элементы, находящиеся на главной диагонали отличаются от нуля

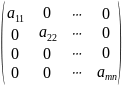
- диагональная матрица второго порядка

Если у диагональной матрицы все числа равны между собой, то она называется скалярной.

Если в скалярной матрице все числа главной диагонали равны числу 1, то матрица называется единичной и обозначается E.

– Единичная матрица третьего порядка

Матрица, все элементы которой равны 0, называется нулевой матрицей и обозначается 0.

– нулевая матрица второго порядка.

В прямоугольной матрице типа возможны случаи:

1. m=1

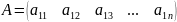– матрица-строка.

2. n=1

– матрица-столбец.

Такие виды матрицы будем называть векторными.

Равенство матриц.

Две матрицы называются равным, если они имеют одинаковое количество строк m, и одинаковое количество столбцов n и их соответствующие элементы равны

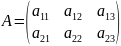
Если в матрице типа переставить строки со столбцом, то получим матрицу типа 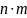, которая называется транспонированной матрицей.

Линейные операции.

Сумма матрицA и B=C, элементы которой равны сумме соответствующих элементов матриц A и B.

Замечание.

Складывать матрицы можно только одного типа.

Пример:

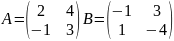
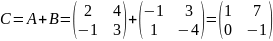
Свойства сложения матриц:

1. A+B=B+A

2. (A+B)+C=A+(B+C)

Из первого и второго свойств следует A+0=A.

Для любой матрицы A существует (-A) такая, что A+(-A)=0

Матрица ­(-A) является противоположной матрице A.

Произведение матрицы A на число kравно матрице, каждый элемент которой равен

Произведение матриц

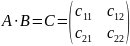
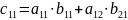
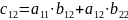
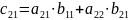
Чтобы получить элемент, состоящий из i-ой строки и j-го столбца матрицей произведения нужно все элементы i-ой строки матрицы A умножить на соответствующий элемент j-го столбца матрицы Bи полученное произведения сложить.

Правила умножения прямоугольных матриц.

Умножение 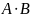имеет смысл только тогда, когда число столбцов матрицы Aравно числу строк матрицы B, в результате умножения двух прямоугольных матриц получается матрица содержащий столько строк, сколько строк в первой матрице и столько столбцов, сколько столбцов во второй матрице.

Свойства умножения матриц.

1. 

2. 

3. 

Определение.

Пусть дана квадратная матрица

Определителем или детерминантом второго порядка называется число равной

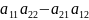
Пишут:

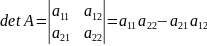
Определение.

Пусть дана матрица третьего порядка

Определителем или детерминантом третьего порядка называется число равной

При вычислении определители третьего порядка удобно пользоваться правило треугольников (Правила Саррус)

Основные свойства определителей.

1. Определитель не изменится если его строки поменять местами с соответствующими столбцами (т.е. транспонировать)

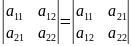
2. При переставлении двух строк или столбцов определитель изменит свой знак на противоположный

3. Общий множитель всех строк элементов строк или столбца можно вывести за знак определителя

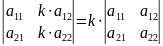
4. Определитель с двумя одинаковыми строками или столбцами равен 0

Пример:

5. Если все элементы двух строк или столбцов определителя пропорциональны, то определитель равен нулю.

6. Если какой-либо строки или столбцов определителя прибавить соответствующие элементы строки им столбца умноженное на одно и то же число, то определитель не изменится.

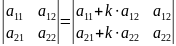
7. Треугольный определитель у которого все элементы лежащие выше или ниже главной диагонали – нули, равен произведению элементов главной диагонали.

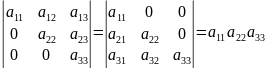
Билет № 16 Решение систем линейных алгебраических уравнений. Прямые методы. Метод Гаусса