
Блок-схема метода касательных
F
начало
(x0)*F”(x0)0
a, b, , m
F(x0)*F”(x0)0
+ -

x0:=b
x0:=a
x:=x0
y= х -
=
корень=, y,
погр.=,
x:=y
y:=х -
=
конец
+ -

Билет №11 Программная реализация метода касательных
Programmet_kasat;
function f (t:real): real;
begin
f:=sin (2*t); {любая}
end;
function f1 (t:real): real;
begin
f1:=2*cos(2*t);
end;
function f2 (t:real): real; {2 произв.}
begin
f2:=-4*sin(2*t);
end;
var a, b, e, m, x, y, x0, d: real
begin
writeln (введите a, b, e, m); readln (a, b, e, m);
if f(a)*f2(a)0 then x0:=a
else x0:=b;
x:=x0;
y:=x-f(x)/f1(x)
d:=(abs(f(y))/m
while d0 do begin
x:=y
y:=x-f(x)/f1(x)
d:=(abs(f(y))/m
end
writeln (корень=, у, погр.=, );
end.
Билет №12 Численное решение нелинейных уравнений с одной переменной. Метод простой итерации
Метод простой интерации
Пусть уравнение имеет единственный корень на отрезке [a,b]. Заменим уравнение F(x) = 0 равносильным уравнением x = f(x) (2)
Пусть ڈ (Кси) =корень уравнения (2), а х0 полученное каким либо способом грубое приближение к корню кси. Подставляя х0 в правую часть уравнения (2) получим некоторое число х1=f(х0). Проделаем тоже самое с x1 и получим х2 = f(х1) и т.д. Последовательно применяя рекуррентное соотношение xn=
= f(xn-1) для n=1,2,…
образуем числовую последовательность х0, x1, х2, х3,... ,хn,…(3)
Последовательность (3) называется последовательностью приближений или итерационной последовательностью. («итерация» - повторение).
Процесс построения итерационной последовательности имеет геометрическую интерпретацию.
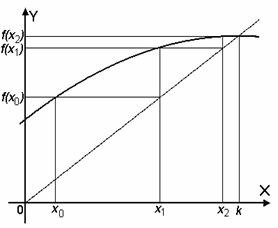
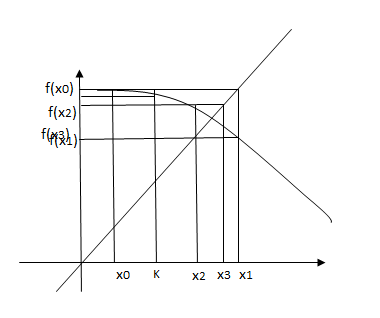
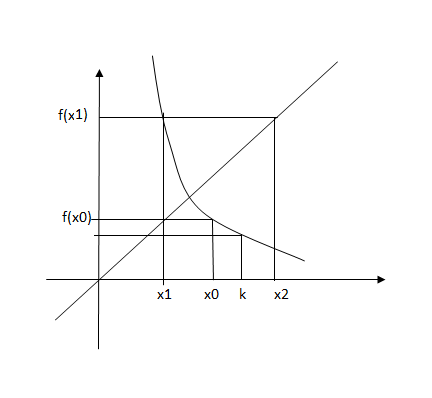
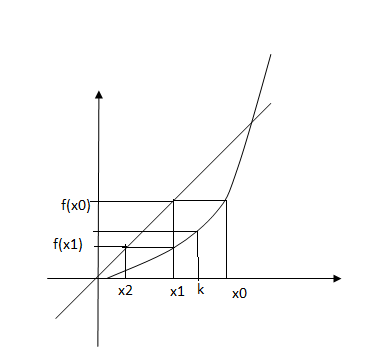
Если последовательность 3 сходится, а функция f(x) непрерывна, то предел последовательности 3 является корнем уравнения 2.
Достаточные условия сходимости итерационного процесса выясняются следующей теоремой:
Теорема:
Пусть уравнение x=f(x) имеет единственный корень на отрезке [a;b] и выполнены условия:
1. f(x) определена и дифференцируема на этом отрезке
2. для всех x из отрезка [a;b] функция f(x) принадлежит [a;b]
3.существует такая правильная дробь q, что для всех x из отрезка [a;b] выполнено условие |f'(x)|<=q<1. Тогда итерационная последовательность xn = f(xn-1).N=1,2,…
Тогда итерационная последовательность сходится при любом начальном xnпринадлежащим[a;b].
Без доказательства
Замечание:
Условия теоремы не являются необходимыми, это означает, что итерационная последовательность (3) может оказаться сходящейся и при не выполнении этих условий.
Пусть уравнение x=f(x) решается методом простой итерации, причем результат должен быть получен с точностью . Критическим для прекращения является условие Δxn≤. (4)
Δxn= (5)
(5)
q-
правильная дробь.
Замечание:
Важное свойство итерационных методов решения уравнений называется самоисправляемостью. Это означает, что если в процессе вычисления приближений допускались ошибки, то они не влияют на окончательный результат.
Билет №13 Алгоритм решения задачи методом простой итерации
Алгоритм решения уравнения методом простой итерации с точностью ε.
Отделение корней. Используется графический метод.
За начальное приближение х0 берется любая точка [a;b].
Приведение уравнения F(x)=0 к виду x=f(x) и проверка условий сходимости итерационного процесса – уравнение F(x)=0 можно привести к виду x=f(x) разными способами, однако, это должно быть сделано так, чтобы для функции f(x) выполнялись условия 1-3 теоремы.
Уравнение F(x)=0 может быть приведено к виду x=f(x) разными способами, однако это должно быть сделано так, чтобы выполнялись условия теоремы. Рассмотрим простейший способ такого преобразования.
Уравнение F(x)=0 преобразуем к виду x=x-m*F(x), где m – отличная от нуля константа. В этом случае f(x)=x-m*F(x).
f’(x)=1-m*F'(x)
Для того чтобы было | f’(x)|=| 1-m*F'(x)|<=q<1 lостаточно подобрать число m, так чтобы для всех x из [a,b] значением выражения m*F'(x) была положительная правильная дробь.
Расчет (уже написали).
