8. Закон сохранения механической энергии. Диссипация энергии.

Закон сохранения механической энергии.
Сумма кинетической и потенциальной энергий системы тел называется полной механической энергиейсистемы.	E = Ep + Ek
Учитывая, что при совершении работы A = Ek и, одновременно, A = - Ep, получим: Ek = - Ep или (Ek + Ep)=0 - изменение суммы кинетической и потенциальной энергий (т.е. изменение полной механической энергии) системы равно нулю.	Ek = - Ep
Значит, полная энергия системы остается постоянной:   E = Ep + Ek = const. В замкнутой системе, в которой действуют только консервативные силы, механическая энергия сохраняется. (Или: полная механическая энергия системы тел, взаимодействующих силами упругости и гравитации, остается неизменной при любых взаимодействиях внутри этой системы).	E = Ep + Ek = const
Например, для тела, движущегося под действием силы тяжести (падение; тело, брошенное под углом к горизонту, вертикально вверх или движущееся по наклонной плоскости без трения):  .

Диссипация энергии (лат. dissipatio — рассеяние) — переход части энергии упорядоченных процессов (кинетической энергии движущегося тела, энергии электрического тока и т. п.) в энергию неупорядоченных процессов, в конечном счёте — в теплоту. Системы, в которых энергия упорядоченного движения с течением времени убывает за счёт диссипации, переходя в другие виды энергии, например в теплоту или излучение, называются диссипативными. Для учёта процессов диссипации энергии в таких системах при определённых условиях может быть введена диссипативная функция. Если диссипация энергии происходит в замкнутой системе, то энтропия системы возрастает. Диссипация энергии в открытых системах, обусловленная процессами уноса энергии из системы, например в виде излучения, может приводить к уменьшению энтропии рассматриваемой системы при увеличении полной энтропии системы и окружающей среды. Это, в частности, обеспечивает важную роль процессов диссипации энергии в уменьшении удельной энтропии вещества на стадиях образования галактик и звёзд в модели горячей Вселенной.

9. Момент импульса материальной точки относительно неподвижного центра вращения. Уравнение моментов.

Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:    где r - радиус-вектор, проведенный из точки О в точку A, p=mv - импульс материальной точки (рис. 1); L - псевдовектор, направление которого совпадает с направлением поступательного движения правого винта при его вращении от r к р.

Моментом импульса относительно неподвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса L_z не зависит от положения точки О на оси z.  При вращении абсолютно твердого тела вокруг неподвижной оси z каждая точка тела движется по окружности постоянного радиуса r_iсо скоростью v_i . Скорость v_i и импульс m_iv_i перпендикулярны этому радиусу, т. е. радиус является плечом вектора m_iv_i . Значит, мы можем записать, что момент импульса отдельной частицы равен  (1)  и направлен по оси в сторону, определяемую правилом правого винта.  Монет импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:    Используя формулу v_i = ωr_i, получим    т. е.   2)  Таким образом, момент импульса твердого тела относительно оси равен моменту инерции тела относительно той же оси, умноженному на угловую скорость. Продифференцируем уравнение (2) по времени:    т. е.    Эта формула - еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.  Можно показать, что имеет место векторное равенство  (3)  В замкнутой системе момент внешних сил   и   откуда   (4)  Выражение (4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.  Закон сохранения момента импульса также как и закон сохранения энергии является фундаментальным законом природы. Он связан со свойством симметрии пространства - его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол). 

Уравнение моментов

Предположим, что точка О неподвижна. В случае одной материальной точки, дифференцируя (3), получаем

.

При неподвижной точке О вектор  , равный  , параллелен   и поэтому   . Кроме того  .

Таким образом  . (5)

Э то уравнение моментов для одной материальной точки. Распространим его на систему материальных точек, для чего запишем уравнение (5) для каждой материальной точки механической системы, понимая под М момент всех действующих на нее сил, как внутренних так и внешних. Затем сложим все эти уравнения. Внутренние силы входят в систему попарно так, что  где   - сила воздействия k-й материальной точки на i-ю. Кроме того, эти силы   и  , действуют вдоль одной и той же прямой. Момент таких двух сил, а значит и моменты всех внутренних сил равны нулю. В результате опять получается уравнение моментов типа (5) только для системы материальных точек, в котором  определяется выражением (4), а   - выражением (2) для внешних сил, т. е.

. (6)

Моментом силы механической системы относительно оси называется проекция на эту ось вектора момента силы системы относительно любой точки, выбранной на рассматриваемой оси (рис. 2). Соответственно, моментом импульса относительно оси называется проекция на эту ось вектора момента импульса относительно любой точки на данной оси.

Можно доказать, что выбор точки на оси влияет на значения моментов импульса   и  относительно точки, но не влияет на значения соответствующих проекций моментов на эту ось.

Если мы выбираем прямоугольную систему координат с началом, совпадающим с полюсом, то имеем:

    (7)
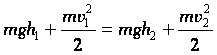