5. Потенциальная энергия в поле тяжести. Потенциальная энергия сжатой (растянутой) пружины.

1)Потенциальная энергия   в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

где   — масса тела,   — ускорение свободного падения,   — высота положения центра масс тела над произвольно выбранным нулевым уровнем.

2)Пусть растянутая пружина закреплена одним концом, а второй конец, перемещаясь, совершает работу. Нужно учитывать, что сила, с которой действует пружина, не остается постоянной, а изменяется пропорционально растяжению. Если первоначальное растяжение пружины, считая от нерастянутого состояния, равнялось  , то первоначальное значение силы упругости составляло  , где  — коэффициент пропорциональности, который называют жесткостью пружины. По мере сокращения пружины эта сила линейно убывает от значения   до нуля. Значит, среднее значение силы равно  . Можно показать, что работа   равна этому среднему, умноженному на перемещение точки приложения силы:

.

Таким образом, потенциальная энергия растянутой пружины

                                                                                 (98.1)

Такое же выражение получается для сжатой пружины.

В формуле (98.1) потенциальная энергия выражена через жесткость пружины и через ее растяжение  . Заменив   на  , где   — упругая сила, соответствующая растяжению (или сжатию) пружины  , получим  выражение

,                                                                         (98.2)

которое определяет потенциальную энергию пружины, растянутой (или сжатой) силой  . Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, т.е. чем больше ее упругость, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной растягивающей, силе. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на перемещение точки приложения силы, т. е. работа.

6. Потенциальная энергия гравитационного взаимодействия.

Потенциальная энергия гравитационного взаимодействия системы двух материальных точек с массами m и M, находящихся на расстоянии  R одна от другой, равна

где G – гравитационная постоянная, а нуль отсчета потенциальной энергии (Е_p = 0) принят при r = ∞.

G — гравитационная постоянная, равна примерно 6,6725×10-11 м³/(кг·с²).

7. Связь потенциальной энергии точки с силой, действующей на точку со стороны потенциального поля. Градиент скалярной функции.

Градиент скалярной функции

Для случая трёхмерного пространства градиентом скалярной функции   координат  ,  ,   называется векторная функция с компонентами

,  ,  .

Или, использовав для единичных векторов по осям прямоугольных декартовых координат  :

Если   — функция   переменных  , то её градиентом называется  -мерный вектор

компоненты которого равны частным производным   по всем её аргументам.

• Размерность вектора градиента определяется, таким образом, размерностью пространства (или многообразия), на котором задано скалярное поле, о градиенте которого идет речь.

• Оператором градиента (обозначаемым обычно, как говорилось выше, 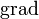  или  ) называется оператор, действие которого на скалярную функцию (поле) дает ее градиент. Этот оператор иногда коротко называют просто "градиентом".

Смысл градиента любой скалярной функции   в том, что его скалярное произведение с бесконечно малым вектором перемещения   дает полный дифференциал этой функции при соответствующем изменении координат в пространстве, на котором определена  , то есть линейную (в случае общего положения она же главная) часть изменения   при смещении на  . Применяя одну и ту же букву для обозначения функции от вектора и соответствующей функции от его координат, можно написать:

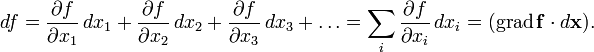
Стоит здесь заметить, что поскольку формула полного дифференциала не зависит от вида координат  , то есть от природы параметров x вообще, то полученный дифференциал является инвариантом, то есть скаляром, при любых преобразованиях координат, а поскольку   — это вектор, то градиент, вычисленный обычным образом, оказываетсяковариантным вектором, то есть вектором, представленным в дуальном базисе, какой только и может дать скаляр при простом суммировании произведений координат обычного (контравариантного), то есть вектором, записанным в обычном базисе. Таким образом, выражение (вообще говоря — для произвольных криволинейных координат) может быть вполне правильно и инвариантно записано как:

или, опуская по правилу Эйнштейна знак суммы,

(в ортонормированном базисе мы можем писать все индексы нижними, как мы и делали выше). Однако градиент оказывается настоящим ковариантным вектором в любых криволинейных координатах.

Связь потенциальной энергии точки с силой, действующей на точку со стороны потенциального поля

Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы  , действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии  . Следовательно, между силой и потенциальной энергией должна существовать определенная связь.

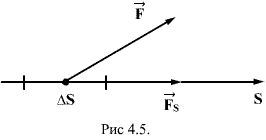
Для установления этой связи вычислим элементарную работу  , совершаемую силами поля при малом перемещении   тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой  . Эта работа равна

где  - проекция силы   на направление  .

Поскольку в данном случае работа совершается за счет запаса потенциальной энергии  , она равна убыли потенциальной энергии   на отрезке оси  :

Из двух последних выражений получаем

Откуда

Последнее выражение дает среднее значение   на отрезке  . Чтобы

получить значение   в точке нужно произвести предельный переход:

Так как   может изменяться не только при перемещении вдоль оси  , но также и при перемещениях вдоль других направлений, предел в этой формул представляет робой так называемую частную производную от   по  :

Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:

Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:

в математике вектор  ,

где а - скалярная функция х, у, z, называется градиентом этого скаляра обозначается символом  .Следовательно сила равна градиенту потенциальной энергии, взятого с обратным знаком