1. Работа сил тяготения и сил гравитационного взаимодействия.

Закон всемирного тяготения

Если взаимодействующие между собой тела можно считать материальными точками или же если они имеют правильную сферическую форму, то формула закона всемирного тяготения имеет вид

F=Gm₁m²/r²  

где F - модуль силы тяготения; m₁ и m₂ - массы материальных точек; r - расстояние между ними; G - коэффициент пропорциональности, называемый постоянной всемирного тяготения или гравитационной постоянной.

Силы, с которыми взаимно притягиваются тела по закону всемирного тяготения, являются центральными, т. е. они направлены вдоль прямой, соединяющей центры взаимодействующих тел.

Гравитационные силы

Из при m₁=m₂=m имеем:

G=Fr²/m².

Из этой формулы видно, что гравитационная постоянная численно равна силе взаимного тяготения двух материальных точек, имеющих массы, равные единице массы, и находящихся друг от друга на расстоянии, равном единице длины. Числовое значение гравитационной постоянной устанавливают экспериментально. Впервые это сделал английский ученый Кэвендиш с помощью крутильного динамометра (крутильных весов).

В СИ гравитационная постоянная имеет значение

G = 6,67·10^-11 Нм²/кг².

Следовательно, две материальные точки массой 1 кг каждая, находящиеся друг от друга на расстоянии 1 м, взаимно притягиваются гравитационной силой, равной 6,67·10^-11 Н.

Работа сил тяготения

Изучая притяжение тел по закону всемирного тяготения, мы встречаемся с гравитационным взаимодействием между телами. Это взаимодействие является одним из видов фундаментальных взаимодействий, существующих в природе. Оно осуществляется на расстоянии без непосредственного контакта между взаимодействующими телами.

Согласно представлениям материалистической науки, любое взаимодействие тел на расстоянии осуществляется посредством материальной среды, называемой полем (и поле, и вещество являются формами существования материи).

Гравитационное взаимодействие между телами, описываемое законом всемирного тяготения, осуществляется посредством гравитационного поля (поля тяготения). В каждой точке поля тяготения на помещенное туда тело действует сила тяготения, пропорциональная массе этого тела. Сила тяготения не зависит от среды, в которой находятся тела.

Поле тяготения обладает специфическим свойством, состоящим в том, что при переносе тела массой m из одной точки поля тяготения в другую работа силы тяготения не зависит от траектории движения тела, а зависит только от положения в этом поле начальной и конечной точек перемещения тела. Силы, обладающие подобным свойством, называют консервативными, а поле таких сил - потенциальным. Следовательно, поле тяготения является потенциальным полем, а сила тяготения - консервативной силой.

Расчет показывает, что работа силы тяготения А в поле тяготения Земли определяется по формуле

A=GMm(1/r₁-1/r₂)

где m - масса тела; M - масса Земли; r₁ и r₂ - расстояния от центра Земли до начальной и конечной точек перемещения тела.

2. Консервативные (потенциальные) и неконсервативные силы. Условие консервативности (потенциальности) сил.

В физике консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.

Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.

Для консервативных сил выполняются следующие тождества:

 — ротор консервативных сил равен 0;

 — работа консервативных сил по произвольному замкнутому контуру равна 0;

 — консервативная сила является градиентом некой скалярной функции  , называемой силовой. Эта функция равна потенциальной энергии   взятой с обратным знаком. Соответственно,   и   связаны соотношением

Таким образом, потенциальная сила всегда направлена против направления возрастания потенциальной энергии.

В школьной программе по физике силы разделяют на консервативные и неконсервативные. Примерами консервативных сил являются: сила тяжести, сила упругости, сила кулоновского(электростатического) взаимодействия. Примерами неконсервативных сил являются сила трения и сила сопротивления среды.

Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.

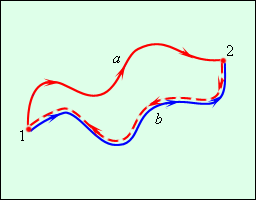
Работа консервативной силы A_1a2 = A_1b2.

Работа на замкнутой траекторииA = A_1a2 + A_2b1 = A_1a2 – A_1b2 = 0