- •Предмет финансовой математики.
- •Проценты. Виды процентных ставок.
- •Расчет процентов. Виды процентных ставок.
- •5.1. Простые проценты
- •Задачи на простые проценты
- •5.2. Сложные проценты
- •Дисконтирование (учет)
- •Задачи на сложные проценты
- •Финансовая рента
- •Будущая стоимость ренты
- •Инфляция
- •Индекс цен Ip или индекс покупательной способности .
- •Два случая учета инфляции
- •Для простых процентов:
- •Финансовые риски и методы их оценки
- •Методы, методология риска
- •Оценка инвестиционных проектов
- •Портфель ценных бумаг
- •Модуль 5. Оценка инвестиционных проектов
- •Чистый приведенный доход npv (net present value)
- •Типовые примеры на расчет показателя чистого приведенного дохода
- •Индекс рентабельности инвестиций pi (profitability index)
- •Норма рентабельности инвестиции irr (Internal rate of return)
- •Irr показывает максимально допустимый относительный уровень доходов, которые могут быть ассоциированы с данным проектом.
- •Срок окупаемости инвестиций рр
- •Модуль 6. Кредиты. Планирование погашения долгосрочной задолженности
- •Планирование погасительного фонда
- •Погашение долга в рассрочку
- •Погашение потребительского кредита
- •Модуль 7. Ценные бумаги Облигации
- •Виды цен облигаций
- •Два источника дохода от облигаций
- •Доходность облигаций
- •Облигации с нулевым купоном
- •Облигации с постоянным доходом
- •Текущая стоимость обыкновенных акций
Задачи на сложные проценты
Задача 5 Вкладчик внес 2 млн. руб. в банк под 50% годовых на 5 лет. Проценты сложные. Какова сумма средств вкладчика по окончании срока? Чему равен доход вкладчика за 5 лет? Решение: Наращенная сумма денег по формуле сложных процентов имеет вид S = P (1 + i) n, где P - сумма кредита; n - срок кредита, лет; i - процентная ставка. Таким образом, сумма средств вкладчика по окончании срока S = 2 (1 + 0,5) 5 = 15,1875 млн. руб. Доход вкладчика J = S - P = 15,1875 - 2 = 13,1875 млн. руб.
|
Задача 6 Через год владелец векселя, выданного коммерческим банком, должен получить по нему 220 тыс. руб. Какая сумма была внесена в банк в момент приобретения векселя, если годовая ставка составляет 120%? Решение: Используем формулу математического дисконтирования
Таким образом, первоначальная сумма составит
|
Финансовая рента
Финансовая рента – это последовательность платежей, выплачиваемых через равные промежутки времени. Промежуток времени между двумя последовательными платежами называется рентным периодом. Время от начала первого рентного периода до конца последнего называют сроком ренты.
Пусть
t
– срок ренты (в годах),
![]() --
количество рентных платежей в году.
Тогда количество всех рентных платежей
(которое мы обозначим буквой n)
можно найти по формуле:
--
количество рентных платежей в году.
Тогда количество всех рентных платежей
(которое мы обозначим буквой n)
можно найти по формуле:
![]()
Если
число рентных платежей не ограничено
(т.е.
![]() ),
рента называется вечной.
),
рента называется вечной.
Рента, в которой рентные платежи осуществляются в конце рентных периодов, называется обыкновенной. Если все рентные платежи одинаковы, рента называется постоянной. Мы ограничимся рассмотрением обыкновенных постоянных рент.
Обозначим через R размер рентного платежа. Временная диаграмма платежей обыкновенной постоянной ренты (с конечным числом платежей) имеет вид:
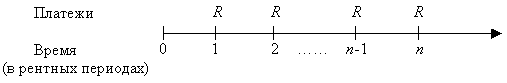
Текущая стоимость ренты
Поскольку финансовая рента – частный случай последовательности платежей, текущая стоимость ренты может быть найдена с помощью формулы (2). Таким образом,
![]()
где r – эффективная процентная ставка для рентного периода.
С помощью формулы для суммы геометрической прогрессии, выражение
несложно привести к следующему виду:
![]()
Пример 1. Пусть рентные платежи, равные 100 д.е., выплачиваются поквартально в течение двух лет. Номинальная годовая процентная ставка равна 16%. Период капитализации процента – полугодие. Требуется определить текущую стоимость ренты. Решение.
Итак,
Найдём
эффективную процентную ставку для
рентного периода:
Теперь мы можем найти текущую стоимость ренты по формуле
В случае вечной ренты с помощью формулы для суммы бесконечной геометрической прогрессии имеем:
Таким образом, в случае вечной ренты
где r – эффективная процентная ставка для рентного периода. |
Пример 2. Пусть рентные платежи, равные 100 д.е., выплачиваются поквартально неограниченное число лет. Номинальная годовая процентная ставка равна 16%. Период капитализации процента – полугодие. Требуется определить текущую стоимость ренты.
Решение.
Итак,
Найдём эффективную процентную ставку для рентного периода: Теперь мы можем найти текущую стоимость ренты по формуле
|

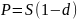
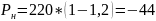
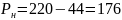 тыс.
руб.
тыс.
руб.