Интервалы монотонности и экстремумы функции

Если производная функции y = f(x) положительна (отрицательна) во всех точках промежутка, то функция y = f(x) монотонно возрастает (убывает) на этом промежутке.

Точка называется точкой максимума (минимума) функции , если существует интервал, содержащий точку , такой, что для всех из этого интервала имеет место неравенство , ( ). Точки максимума и минимума называются точками экстремума.

Необходимое условие экстремума: в точке экстремума функции ее производная либо равна нулю ( ) либо не существует.

Первое достаточное условие экстремума: если в точке функция непрерывна, а производная применить переходе через точку меняет знак, то точка - точка экстремума: максимума, если знак меняется с «+» на «-», и минимума, если с «-» на «+».

Если при переходе через точку производная не меняет знак, то в точке экстремума нет.

Второе достаточное условие экстремума: если в точке , а , то является точкой максимума функции. Если , а , то является точкой минимума функции.

Схема исследования функции на экстремум:

1. найти производную ;

2. найти критические точки функции, в которых производная равна нулю или не существует;

3. исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции;

4. найти экстремальные значения функции;

При исследовании функции на экстремум с помощью 2-го достаточного условия п. 1), 2), 4) сохраняются, а в п. 3) необходимо найти вторую производную и определить ее знак в каждой критической точке.

Чтобы найти наибольшее и наименьшее значение (глобальный максимум и минимум функции ) на отрезке , следует выбрать наибольшее (наименьшее) из значений функции в критических точках, находящихся в интервале и на концах отрезка (в точках и )

Если дифференцируемая на интервале функция имеет единственную точку экстремума, то в этой точке достигается наибольшее и наименьшее значение (глобальный максимум и минимум) функции на интервале .

Интервалы выпуклости функции. Точки перегиба.

Функция называется выпуклой вверх (вниз) на промежутке, если для любых двух значений , из этого промежутка выполняется неравенство:

.

Точки, разделяющие интервалы выпуклости, называется точками перегиба.

Если вторая производная функции положительна (отрицательна) на промежутке, то функция является выпуклой вниз (вверх) на этом промежутке.

Если - точка перегиба функции и существует, то .

Если вторая производная меняет знак при переходе через точку , то точка является точкой перегиба функции .

Схема исследования функции на выпуклость и точки перегиба:

1. найти вторую производную функции ;

2. найти точки, в которых вторая производная 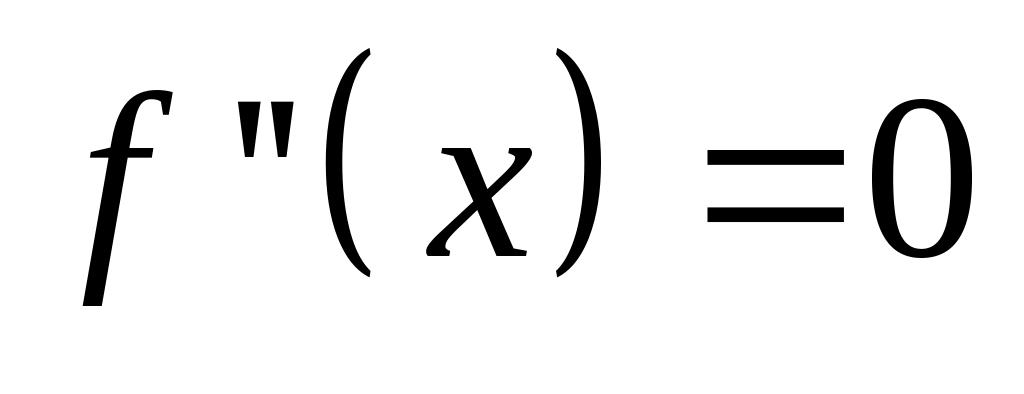или не существует;

3. исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости и наличии точек перегиба;

4. найти значения функции в точках перегиба;