Лекция 5. Производная функции

Производной функции у =f(x) называется конечный предел при­ращения функции к приращению независимой переменной при стрем­лении последнего к нулю (при условии, что этот предел существует):

Если функция в точке x₀ (или на промежутке X) имеет конечную производную, то функция называется дифференцируемой в этой точке (или на промежутке X).

Если функция у = f(x) дифференцируема в точке х₀ (или на промежутке X), то она в этой точке непрерывна (или на промежутке X) Если функция непрерывна в данной точке, то она не обязательно дифференцируема в этой точке.

Правила дифференцирования:

с — постоянная, и = и(х), v = v(x) — дифференцируемые функции:

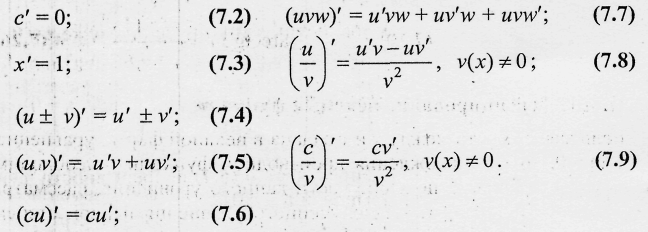
Если у =f(x) — дифференци­руемая и строго монотонная функция на промежутке X, то функция, обратная к данной х = φ(у), также дифференцируема и ее производная определяется соотношением:

Логарифмической производной функции y =f(х) называется производная от логарифма этой функции, т.е.

Формулы дифференцирования основных элементарных функций:

)

Если зависимость между х и у задана в неявной форме уравнением F (х, у) = 0, то для нахождения производной функции у необходимо продифференцировать по х обе части данного уравнения, рассматри­вая у как функцию от х. Из полученного уравнения первой степени относительно y’ находится y’.

Производной п-го порядка называется производная от производ­ной (п - 1)-го порядка. Производные высших порядков вычисляются последовательным дифференцированием данной функции:

Лекция 6. Приложения производной

Геометрический смысл производной. Если кривая задана уравне­нием у =f(x) или F (х, у)= О, то есть угловой коэффициент касательной (тангенс угла ее наклона с положительным направлением си абсцисс).

Уравнение касательной к кривой у =f(x) в точке x₀ имеет вид:

а уравнение нормали:

Механический смысл производной. Если точка движется по за­кону s. = s (t), где s — путь, t — время, то s'(t) представляет скорость изменения пути в момент t. Вторая производная пути по времени s"(i) = [s'(i)]' = v'(f) есть скорость изменения скорости или ускорение точки в момент t.

Теорема (правило Лопиталя). Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле:

Таким образом, правило Лопиталя используется для раскрытия неопределенностей вида или .

Правило Лопиталя можно применять также и для раскрытия неопределенностей вида . Для этого произведение следует записать в виде (или ) и получить неопределенность вида или .

Если имеется неопределенность вида или , при вычислении предела функции , то логарифм этой функции представляет собой неопределенность вида . При этом используется соотношение (полученное на основе свойств логарифмов и непрерывности показательной функции):