Лекция 3. Функция. Свойства функции

Если каждому элементу (значению) x множества X поставить в соответствие определенный элемент (значение) у множества Y, то го­ворят, что на множестве X задана функция у = f(x); при этом множе­ство X называется областью определения функции у, а множество Y— областью значений функции у.

Функция у = f(x) называется четной, если для любых значений x из области определения функции и нечетной, если В противном случае f(x) — функция общего вида.

Функция у = f(x) называется возрастающей (убывающей) на не­котором промежутке X, если большему значению аргумента соответ­ствует большее (меньшее) значение функции f(x). Возрастающие или убывающие функции называются монотонными.

Функция f(x) называется ограниченной на промежутке X, если существует такое число М > 0, что для всех В про­тивном случае функция называется неограниченной.

Если функция у = f(x) есть функция переменной и (определен­ной на множестве U с областью значений Y), а переменная и, в свою очередь, также является функцией (определенной на множе­стве X с областью значений U), то заданная на множестве X функция у = называется сложной функцией.

Функции, построенные из основных элементарных функций при помощи конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.

Функция у = f{x) называется периодической с периодом если для любых

Преобразования графиков:

а) — сдвигает график параллельно оси Ох на единиц, (а > 0 — влево, а < 0 — вправо);

б) — сдвигает график параллельно оси Оу на единиц b > 0 — вверх, b < 0 — вниз);

в) — растягивает в с раз (c > 1) или сжимает (0 < с < 1) график относительно оси Оу; при с < 0 симметрично отображает график относительно оси Ох;

г) — растягивает в k раз (k > 1) или сжимает (0 < k < 1) график относительно оси Ох; при k < 0 симметрично отобра­жает график относительно оси Оу.

Лекция 4. Предел функции. Непрерывность

Если по некоторому закону каждому натуральному числу п по­ставлено в соответствие определенное число а_n то говорят, что задана числовая последовательность .

Число А называется пределом числовой последовательности , если для любого  > 0 найдется такой номер N, зависящий от , что для всех членов последовательности с номерами п > N верно неравенство

Число А называется пределом функции у=f(x) при если для любого  > 0 найдется также число S > 0, зависящее от , что для всех х таких, что |х| > S, будет верно неравенство .

Число А называется пределом функции f (х) при если для любого  > 0 найдется число  > 0, зависящее от , что для всех и удовлетворяющих условию выполняется неравенство

Теоремы о пределах:

1) (С-постоянная).

2) Если то:

Если то .

Первый замечательный предел:

Второй замечательный предел (число е):

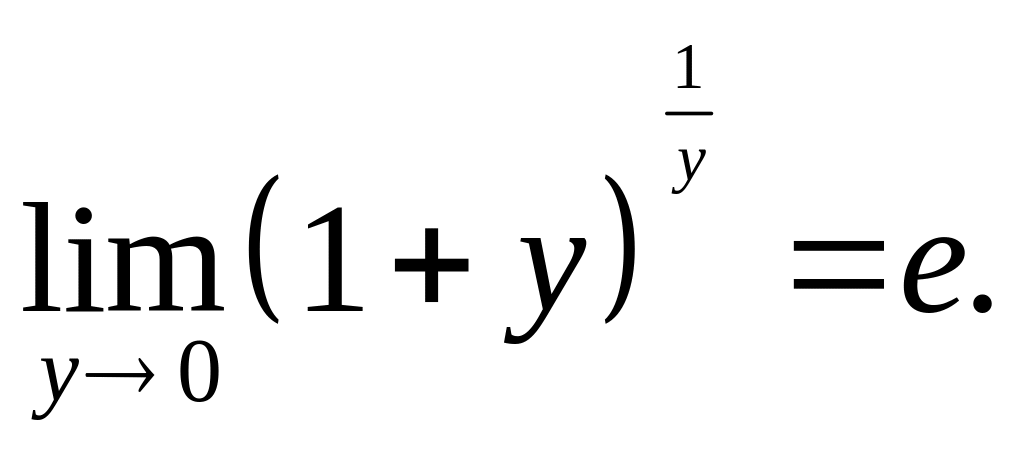
Функция называется непрерывной в точке хо, если она удовле­творяет следующим условиям: 1) определена в точке , 2) имеет конечный предел при х  ; 3) этот предел равен значению функции в этой точке:

(первое определение).

Функция f(x) называется непрерывной в точке , если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:

(второе определение).

Если функции и непрерывны в точке, то их сумма, про­изведение и частное (при условии, что знаменатель отличен от нуля) являются функциями, непрерывными в этой точке.

Если функция непрерывна в точке , а функция непрерывна в точке , то сложная функция непре­рывна в точке -

Функция называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка. Все элемен­тарные функции непрерывны во всех точках, где они определены.

Если не выполнено определение непрерывности (6.4) или (6.5), то функция в точке терпит разрыв, причем:

а) если хотя бы один из односторонних пределов или бесконечен, то - точка разрыва второго рода;

б) если оба односторонних предела и конечны, но не равны между собой, то — точка неустранимого раз­рыва первого рода;

в) если оба односторонних предела и конечны, равны между собой, но не равны , то — точка устрани­мого разрыва первого рода.